摘要：1．设实数x.y满足x2+(y-1)2=1,若对满足条件的x.y.x+y+c0恒成立.则c的取值范围是 A[-1.+) B (-.-1] C [+1.+) D (-.-1]
网址：http://m.1010jiajiao.com/timu3_id_510874[举报]
设函数h(x)＝x2，
(x)＝2elnx(e为自然对数的底)．
(1)求函数F(x)＝h(x)－x的极值；
(2)若存在常数k和b，使得函数f(x)和g(x)对其定义域内的任意实数x分别满足f(x)≥kx＋b和g(x)≤kx＋b，则称直线l：y＝kx＋b为函数f(x)和g(x)的“隔离直线”．试问：函数h(x)和(x)是否存在“隔离直线”？若存在，求出“隔离直线”方程；若不存在，请说明理由．
(1)设x、y、z1∈R，且x＋y＋z＝1，求证x2＋y2＋z2≥
；
(2)设二次函数f(x)＝ax2＋bx＋c(a＞0)，方程f (x)－x＝0有两个实根x1，x2，且满足：0＜x1＜x2＜
，若x∈(0，x1)．
求证：x＜f(x)＜x1
（12分）（1）设x、y、z
R，且x＋y＋z＝1，求证x2＋y2＋z2≥
；
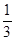（2）设二次函数f (x)＝ax2＋bx＋c （a＞0），方程f (x)－x＝0有两个实根x1，x2，
且满足：0＜x1＜x2＜
，若x(0，x1)。
求证：x＜f (x)＜x1
查看习题详情和答案>>
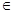R，且x＋y＋z＝1，求证x2＋y2＋z2≥
；
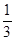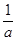，若x
满足：（1）对
有
，即
，使得xo >a（xo <a），即
．给出如下命题：
；
，y∈B}，则