3、掌握三角函数图象的变换及对称性,会利用三角函数图象解决有关问题.
[例题讲解]
例题1
(1)函数 的最小正周期为
( )
的最小正周期为
( )
A
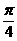 B
B 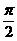 C
C 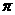 D 2
D 2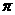
(2)函数 在下列哪个区间内为增函数 ( )
在下列哪个区间内为增函数 ( )
A
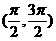 B
B 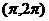 C
C 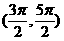 D
D
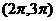
(3)函数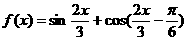 的图象相邻两条对称轴间的距离为( )
的图象相邻两条对称轴间的距离为( )
A
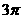 B
B 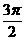 C
C 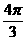 D
D 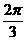
(4)使函数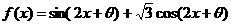 是奇函数,且在[0,
是奇函数,且在[0,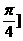 上是减函数的
上是减函数的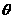 的一个值是 ( )
的一个值是 ( )
A
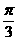 B
B 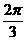 C
C 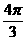 D
D 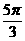
(5)设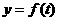 是某港口水的深度y(米)关于时间t(时)的函数,其中
是某港口水的深度y(米)关于时间t(时)的函数,其中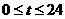 ,下表是该港口某一天从0时至24时记录的时间t与水深y的关系:
,下表是该港口某一天从0时至24时记录的时间t与水深y的关系:
|
t |
0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
|
y |
12 |
15.1 |
12.1 |
9.1 |
11.9 |
14.9 |
11.9 |
8.9 |
12.1 |
经长期观察,函数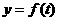 的图象可近似地看成函数
的图象可近似地看成函数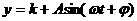 的图象,在下列的函数中,最能近似表示表中数据间对应关系的函数是 ( )
的图象,在下列的函数中,最能近似表示表中数据间对应关系的函数是 ( )
A
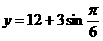
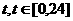 B
B 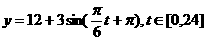
C
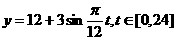 D
D 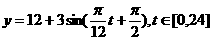
(6)关于函数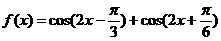 有下列命题:
有下列命题:
①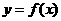 的最大值是
的最大值是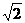 ; ②
; ②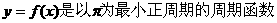 ;
;
③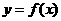 在区间[
在区间[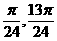 ]上单调递减; ④将函数
]上单调递减; ④将函数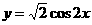 的图象向左平移
的图象向左平移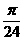 个单位后,将与已知函数的图象重合.
个单位后,将与已知函数的图象重合.
其中真命题的序号为 .
例题2
求函数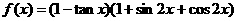 的定义域,值域和最小正周期.
的定义域,值域和最小正周期.
例题3
已知函数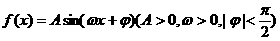 的图像在y轴上的截距为1,它在y轴右侧的第一个最大值点与最小值点分别为
的图像在y轴上的截距为1,它在y轴右侧的第一个最大值点与最小值点分别为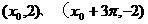 .
.
(1)求函数 的解析式;
的解析式;
(2)求函数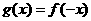 的单调递增区间.
的单调递增区间.
例题4
已知函数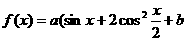 ).
).
(1)当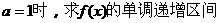 ;
;
(2)当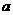 <0,且
<0,且 .
.
例题5
已知函数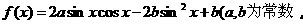
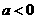 )的图象过点
)的图象过点
(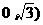 ,且函数最大值为2.
,且函数最大值为2.
(1)求 的解析式,并写出其单调增区间;
的解析式,并写出其单调增区间;
(2)若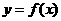 的图象按向量
的图象按向量 作移动距离最小的平移后使所得的图象关于y轴对称,求出向量
作移动距离最小的平移后使所得的图象关于y轴对称,求出向量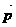 的坐标及平移后的图象对应的解析式.
的坐标及平移后的图象对应的解析式.
高三数学第二轮复习教学案
第二课时:三角式的化简与求值
班级 学号 姓名
[考纲解读]
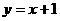 与双曲线
与双曲线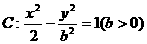 恒有公共点
恒有公共点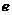 的取值范围
的取值范围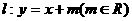 过双曲线C的右焦点
过双曲线C的右焦点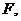 与双曲线交于
与双曲线交于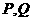 两点,并且满足
两点,并且满足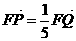 ,求双曲线C的方程.
,求双曲线C的方程.