3.培养解决含参数不等式问题的能力.
例题讲解
例题1
(1) 下列命题为真命题的是 ( )
A 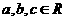 且
且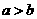 ,则
,则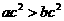 ; B
; B 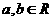 且
且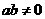 ,则
,则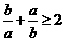 ;
;
C 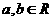 且
且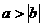 ,则
,则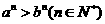 ;
D 若
;
D 若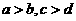 ,则
,则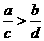 .
.
(2)不等式组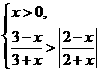 的解集是 ( )
的解集是 ( )
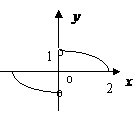 A
A 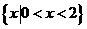 B
B
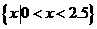
|
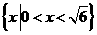 D
D
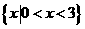
|
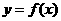 的图象是中心在原点,焦点在
的图象是中心在原点,焦点在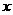 轴上的椭圆
轴上的椭圆
的两段弧,则不等式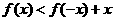 的解集为 ( )
的解集为 ( )
A 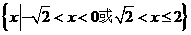 B
B 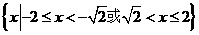
C 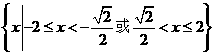 D
D 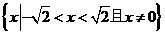
(4) 命题P:关于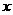 的不等式
的不等式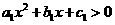 与
与 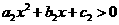 的解集相同;
的解集相同;
命题Q: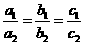 .则P是Q的 ( )
.则P是Q的 ( )
A 充要条件 B充分但不必要条件
C必要但不充分条件 D 既不充分也不必要条件
(5) 如果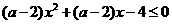 对任意的实数
对任意的实数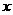 总成立,则
总成立,则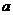 的取值范围是______.
的取值范围是______.
(6) 三个数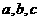 成等比数列,若
成等比数列,若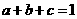 成立,则
成立,则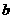 的取值范围为______.
的取值范围为______.
例题2
解关于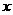 的不等式
的不等式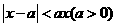
例题3
若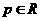 ,且当
,且当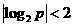 时,不等式
时,不等式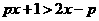 恒成立,试求
恒成立,试求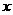 的取值范围.
的取值范围.
例题4
已知二次函数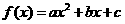 的图象经过
的图象经过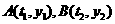 两点,且满足
两点,且满足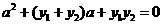 .
.
(1)
证明: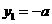 或
或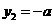 ;
;
(2)
证明:函数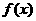 的图象必与
的图象必与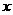 轴有两个不同的交点;
轴有两个不同的交点;
(3)
若关于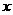 的不等式
的不等式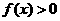 的解集为
的解集为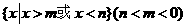 ,解关于
,解关于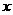 的不等式
的不等式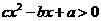
例题5
已知函数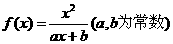 ,且方程
,且方程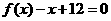 有两个实根为
有两个实根为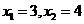 .
.
(1)求函数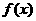 的解析式;
的解析式;
(2)设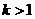 ,解关于
,解关于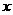 的不等式
的不等式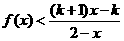
 .
.
高三数学第二轮复习教学案
第十一课时:不等式综合应用
班级 学号 姓名
考纲解读
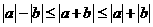 ;
; }中a
}中a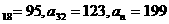 则n 等于 (
)
则n 等于 (
)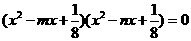 的四个根组成一个首项为
的四个根组成一个首项为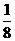 的等比数列,则
的等比数列,则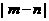 =
(
)
=
(
)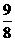 B
1 C
B
1 C 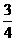 D
D
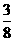
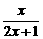 ,满足xn=f(xn-1), (n>1, n∈N*)且x1=f(2),则x10的值为(
)
,满足xn=f(xn-1), (n>1, n∈N*)且x1=f(2),则x10的值为(
)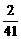 B
B 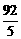 C
C 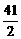 D
D
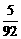
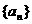 的公比为q,前n项和为Sn,若Sn+1,Sn,Sn+2成等差数列,则q的值为 .
的公比为q,前n项和为Sn,若Sn+1,Sn,Sn+2成等差数列,则q的值为 .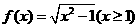 的反函数为
的反函数为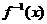 ,数列
,数列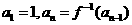
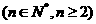 则数列
则数列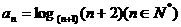 ,若乘积
,若乘积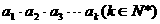 为整数m,则称k为“希望数”,则区间[1,2005]内所有希望数之和为
.
为整数m,则称k为“希望数”,则区间[1,2005]内所有希望数之和为
.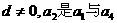 的等比中项.已知数列
的等比中项.已知数列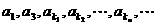 成等比数列,求数列
成等比数列,求数列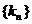 的通项
的通项
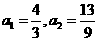 且当
且当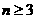 时,
时,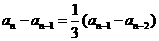 求数列
求数列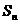 是它的前n项的和,并且
是它的前n项的和,并且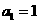 ,
,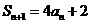 (
(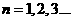 )
)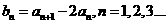 则数列
则数列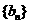 为等比数列;
为等比数列;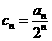
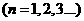 ,则数列
,则数列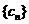 为等差数列;
为等差数列;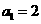 ,前n项和为Sn,在平面直角坐标系
,前n项和为Sn,在平面直角坐标系 中,点
中,点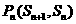 总在曲线
总在曲线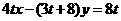 上,其中
上,其中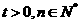 .问:
.问: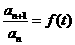 ,数列
,数列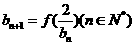 ,
,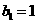 ,求
,求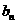 ;
;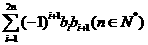 .
.