19.(本小题13分)
解: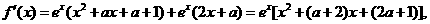
令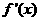 =0得
=0得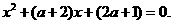
(1)当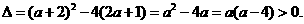
即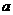 <0或
<0或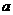 >4时
>4时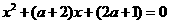 有两个不同的实根
有两个不同的实根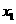 ,
,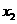 ,不妨设
,不妨设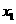 <
<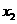
于是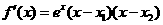 ,从而有下表
,从而有下表
|
x |
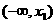 |
x1 |
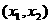 |
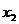 |
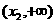 |
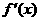 |
+ |
0 |
- |
0 |
+ |
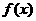 |
↑ |
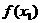 为极大值 为极大值 |
↓ |
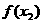 为极小值 为极小值 |
↑ |
即此时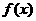 有两个极值点.
有两个极值点.
(2)当△=0即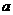 =0或
=0或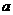 =4时,方程
=4时,方程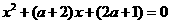 有两个相同的实根
有两个相同的实根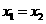
于是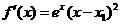
故当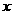 <
<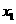 时
时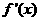 >0,当
>0,当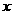 >
>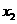 时
时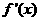 >0,因此
>0,因此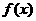 无极值
无极值
(3)当△<0即0<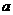 <4时
<4时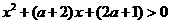
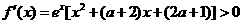 ,故
,故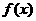 为增函数,此时
为增函数,此时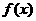 无极值. 因此当
无极值. 因此当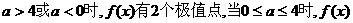 无极值点.
无极值点.
21. (山东卷)已知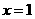 是函数
是函数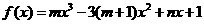 的一个极值点,其中
的一个极值点,其中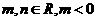 ,
,
(I)求 与
与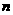 的关系式;
的关系式;
(II)求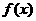 的单调区间;
的单调区间;
(III)当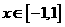 时,函数
时,函数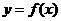 的图象上任意一点的切线斜率恒大于3
的图象上任意一点的切线斜率恒大于3 ,求
,求 的取值范围.
的取值范围.
解(I)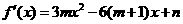 因为
因为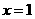 是函数
是函数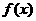 的一个极值点,所以
的一个极值点,所以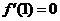 ,即
,即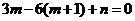 ,所以
,所以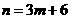
(II)由(I)知,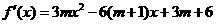 =
=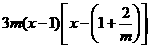
当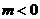 时,有
时,有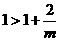 ,当
,当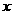 变化时,
变化时,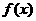 与
与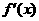 的变化如下表:
的变化如下表:
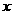 |
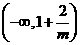 |
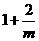 |
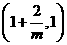 |
1 |
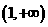 |
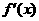 |
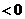 |
0 |
 |
0 |
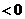 |
|
|
|
|
|
|
|
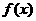 |
调调递减 |
极小值 |
单调递增 |
极大值 |
单调递减 |
故有上表知,当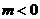 时,
时,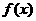 在
在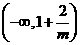 单调递减,在
单调递减,在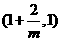 单调递增,在
单调递增,在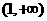 上单调递减.
上单调递减.
(III)由已知得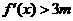 ,即
,即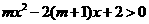
又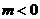 所以
所以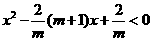 即
即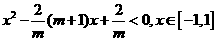 ①
①
设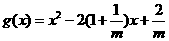 ,其函数开口向上,由题意知①式恒成立,
,其函数开口向上,由题意知①式恒成立,
所以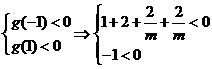 解之得
解之得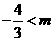 又
又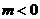 所以
所以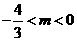
即 的取值范围为
的取值范围为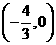
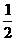 (B)
(B) 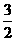 (C)
(C) 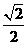 (D)
(D)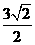
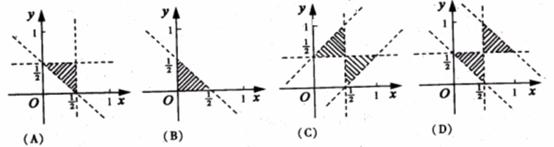
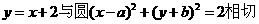 ”的 (A )
”的 (A )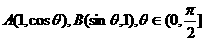 ,则当△OAB的面积达最大值时,
,则当△OAB的面积达最大值时,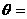 ( D
)
( D
)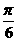 B.
B.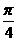 C.
C.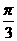 D.
D.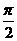
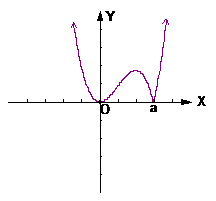
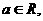 函数
函数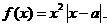
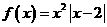 ,则方程f(x)=x即为
,则方程f(x)=x即为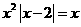
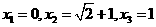

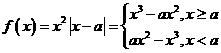 ,
,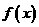 有两个极值点
有两个极值点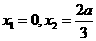 借助于图像可知
借助于图像可知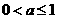 时,函数
时,函数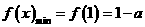
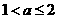 时,显然此时函数的最小值为
时,显然此时函数的最小值为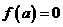
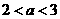 时,
时,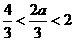 ,此时
,此时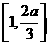 为增函数,在区间
为增函数,在区间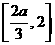 上为减函数,∴
上为减函数,∴ ,又可得
,又可得
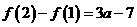
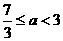 时,
时,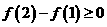 ,此时
,此时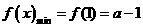
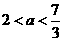 时,
时,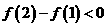 ,此时
,此时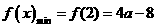
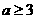 时,
时,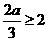 ,此时
,此时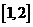 为增函数,故
为增函数,故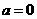 时,
时,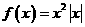 ,此时
,此时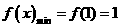
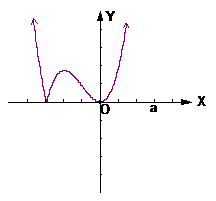
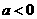 时,其草图见右
时,其草图见右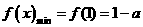
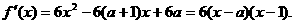
 取得极值, 所以
取得极值, 所以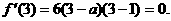 解得
解得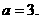
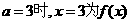 为极值点.
为极值点.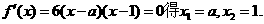
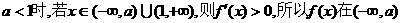 和
和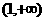 上为增函数,故当
上为增函数,故当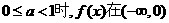 上为增函数.
上为增函数.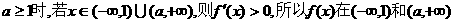 上为增函数,从而
上为增函数,从而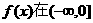 上也为增函数.
上也为增函数. 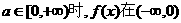 上为增函数.
上为增函数.