2.解题策略:
解探索性问题应注意三个基本问题:认真审题,确定目标;深刻理解题意;开阔思路,发散思维,运用观察、比较、类比、联想、猜想等带有非逻辑思维成分的合理推理,以便为逻辑思维定向.方向确定后,又需借助逻辑思维,进行严格推理论证,这两种推理的灵活运用,两种思维成分的交织融合,便是处理这类问题的基本思想方法和解题策略
解决探索性问题,对观察、联想、类比、猜测、抽象、概括诸方面有较高要求,高考题中一般解这类问题有如下方法:
(1)直接法:直接从给出的结论入手,寻求成立的充分条件;直接从给出的条件入手,寻求结论;假设结论存在(或不存在),然后经过推理求得符合条件的结果(或导出矛盾)等
例1.如图,在直四棱柱A1B1C1D1-ABCD中,当底面四边形ABCD满足条件__________时,有A1C⊥B1D1(注:填上你认为正确的条件即可,不必考虑所有可能的情况)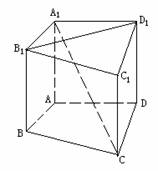
分析:本题是条件探索型试题,即寻找结论A1C⊥B1D1成立的充分条件,由AA1⊥平面A1C1以及A1C⊥B1D1(平面A1C1的一条斜线A1C与面内的一条直线B1D1互相垂直),容易联想到三垂线定理及其逆定理。因此,欲使A1C⊥B1D1,只需B1D1与CA1在平面A1C1上的射影垂直即可。显然,CA1在平面A1C1上的射影为A1C1,故当B1D1⊥A1C1时,有A1C⊥B1D1,又由于直四棱柱的上、下底面互相平行,从而B1D1∥BD,A1C1∥AC。因此,当BD⊥AC时,有A1C⊥B1D1。由于本题是要探求使A1C⊥B1D1成立的充分条件,故当四边形ABCD为菱形或正方形时,依然有BD⊥AC,从而有A1C⊥B1D1,故可以填:①AC⊥BD或②四边形ABCD为菱形,或③四边形ABCD为正方形中的任一个条件即可。
点评: AC⊥BD是结论A1C⊥B1D1成立的充要条件,而所填的ABCD是正方形或菱形则是使结论A1C⊥B1D1成立的充分而不必要的条件. 本例中,满足题意的充分条件不唯一,具有开放性特点,这类试题重在考查基础知识的灵活运用以及归纳探索能力。
例2.(2000年全国高考试题)如图,E、F分别为正方体的面ADD1A1和面BCC1B1的中心,则四边形BFD1E在该正方体的面上的射影可能是_____________(要求把可能的图形的序号都填上)
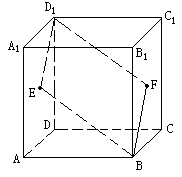
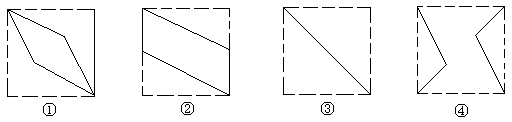
分析:本题为结论探索型的试题,要求有一定的空间想象能力。
解:由于正方体的6个面可分为互为平行的三对,而四边形BFD1E的在互为平行的平面上的射影相同,因此可把问题分为三类:a:在上、下两面上的射影为图②;b:在前、后两面上的射影为图②;c:在左、右两面上的射影为图③.
综上可知,在正方体各面上的射影是图②或图③。
点评:这也是一道结论探索型问题,结论不唯一,应从题设出发,通过分类以简化思维,再利用射影的概念,得到正确的结论。
例3.已知函数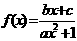 (a,c∈R,a>0,b是自然数)是奇函数,f(x)有最大值
(a,c∈R,a>0,b是自然数)是奇函数,f(x)有最大值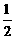 ,且f(1)>
,且f(1)>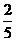 .(1)求函数f(x)的解析式;(2)是否存在直线l与y=f(x)的图象交于P、Q两点,并且使得P、Q两点关于点(1,0)对称,若存在,求出直线l的方程,若不存在,说明理由.
.(1)求函数f(x)的解析式;(2)是否存在直线l与y=f(x)的图象交于P、Q两点,并且使得P、Q两点关于点(1,0)对称,若存在,求出直线l的方程,若不存在,说明理由.
分析:本题考查待定系数法求函数解析式、最值问题、直线方程及综合分析问题的能力.
解:(1)∵f(x)是奇函数
∴f(–x)=–f(x),即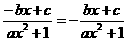 ,∴–bx+c=–bx–c,∴c=0
,∴–bx+c=–bx–c,∴c=0
∴f(x)=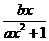 .由a>0,b是自然数得当x≤0时,f(x)≤0,
.由a>0,b是自然数得当x≤0时,f(x)≤0,
当x>0时,f(x)>0,∴f(x)的最大值在x>0时取得.
∴x>0时,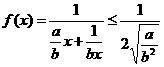 当且仅当
当且仅当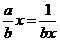
即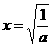 时,f(x)有最大值
时,f(x)有最大值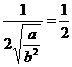 ∴
∴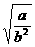 =1,∴a=b2
①
=1,∴a=b2
①
又f(1)>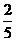 ,∴
,∴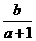 >
>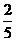 ,∴5b>2a+2 ②
,∴5b>2a+2 ②
把①代入②得2b2–5b+2<0解得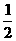 <b<2,又b∈N,∴b=1,a=1,∴f(x)=
<b<2,又b∈N,∴b=1,a=1,∴f(x)=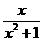
(2)设存在直线l与y=f(x)的图象交于P、Q两点,且P、Q关于点(1,0)对称,
P(x0,y0)则Q(2–x0,–y0),∴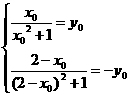 ,消去y0,得x02–2x0–1=0
,消去y0,得x02–2x0–1=0
解之,得x0=1±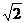 ,∴P点坐标为(
,∴P点坐标为(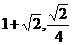 )或(
)或(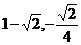 )
)
进而相应Q点坐标为Q(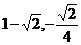 )或Q(
)或Q(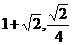 ).
).
过P、Q的直线l的方程:x–4y–1=0即为所求.
点评:充分利用题设条件是解题关键.本题是存在型探索题目,注意在假设存在的条件下推理创新,若由此导出矛盾,则否定假设,否则,给出肯定的结论,并加以论证.
(2)观察--猜测--证明
例4.观察sin220°+cos250°+sin20°cos50°=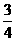 ,sin215°+cos245°+sin15°cos45°=
,sin215°+cos245°+sin15°cos45°=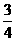 ,
,
写出一个与以上两式规律相同的一个等式 .
答案:sin2α+cos2(α+30°)+sinαcos(α+30°)=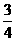
例5.(2003高考上海卷)已知数列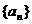 (n为正整数)是首项是a1,公比为q的等比数列.
(n为正整数)是首项是a1,公比为q的等比数列.
(1)求和: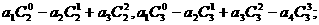
(2)由(1)的结果归纳概括出关于正整数n的一个结论,并加以证明.
(3)设q≠1,Sn是等比数列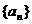 的前n项和,
的前n项和,
求: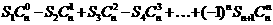
解:(1)
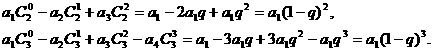
(2)归纳概括的结论为:
若数列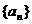 是首项为a1,公比为q的等比数列,则
是首项为a1,公比为q的等比数列,则
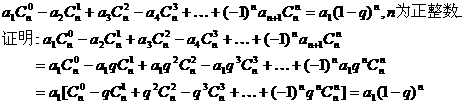
(3)因为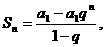
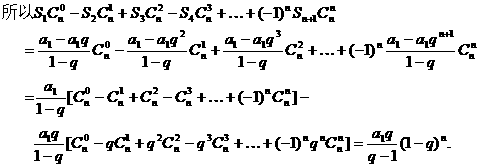
例6.由下列各式:

你能得出怎样的结论,并进行证明.
分析:对所给各式进行比较观察,注意各不等式左边的最后一项的分母特点:1=21-1,3=22-1,7=23-1,15=24-1,…,一般的有2n-1,对应各式右端为一般也有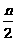 .
.
解:归纳得一般结论
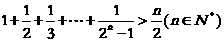
证明:当n=1时,结论显然成立.
当n≥2时,
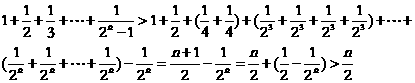
故结论得证.
(3)特殊-一般-特殊:其解法是先根据若干个特殊值,得到一般的结论,然后再用特殊值解决问题。
例7.设二次函数f(x)=ax2+bx+c (a,b,c∈R,a≠0)满足条件:
①当x∈R时,f(x-4)=f(2-x),且f(x)≥x;②当x∈(0,2)时,f(x)≤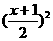
③f(x)在R上的最小值为0。
求最大值m(m>1),使得存在t∈R,只要x∈[1,m],就有f(x+t)≤x
分析:本题先根据题设求出函数f(x)解析式,然后假设t存在,取x=1得t的范围,再令x=m求出m的取值范围,进而根据t的范围求出m的最大值。
解法一:∵f(x-4)=f(2-x),∴函数的图象关于x= -1对称
∴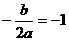 即b=2a
即b=2a
由③知当x= -1时,y=0,即a-b+c=0;由①得 f(1)≥1,由②得 f(1)≤1.
∴f(1)=1,即a+b+c=1,又a-b+c=0
∴a=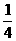 b=
b=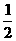 c=
c=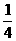 ,∴f(x)=
,∴f(x)=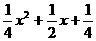
假设存在t∈R,只要x∈[1,m],就有f(x+t)≤x
取x=1时,有f(t+1)≤1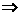
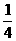 (t+1)2+
(t+1)2+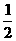 (t+1)+
(t+1)+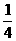 ≤1
≤1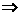 -4≤t≤0
-4≤t≤0
对固定的t∈[-4,0],取x=m,有
f(t+m)≤m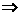
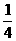 (t+m)2+
(t+m)2+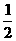 (t+m)+
(t+m)+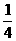 ≤m
≤m m2-2(1-t)m+(t2+2t+1)≤0
m2-2(1-t)m+(t2+2t+1)≤0
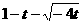 ≤m≤
≤m≤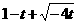 ∴m≤
∴m≤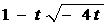 ≤
≤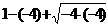 =9
=9
当t= -4时,对任意的x∈[1,9],恒有f(x-4)-x=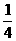 (x2-10x+9)=
(x2-10x+9)=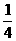 (x-1)(x-9)≤0
(x-1)(x-9)≤0
∴m的最大值为9.
解法二:∵f(x-4)=f(2-x),∴函数的图象关于x=-1对称
∴ 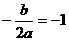 b=2a
b=2a
由③知当x= -1时,y=0,即a-b+c=0;由①得 f(1)≥1,由②得 f(1)≤1
∴f(1)=1,即a+b+c=1,又a-b+c=0
∴a=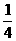 b=
b=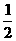 c=
c=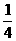 ∴f(x)=
∴f(x)=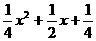 =
=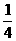 (x+1)2
(x+1)2
由f(x+t)=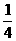 (x+t+1)2≤x 在x∈[1,m]上恒成立
(x+t+1)2≤x 在x∈[1,m]上恒成立
∴4[f(x+t)-x]=x2+2(t-1)x+(t+1)2≤0当x∈[1,m]时,恒成立
令 x=1有t2+4t≤0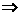 -4≤t≤0
-4≤t≤0
令x=m有t2+2(m+1)t+(m-1)2≤0当t∈[-4,0]时,恒有解
令t= -4得,m2-10m+9≤0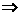 1≤m≤9
1≤m≤9
即当t=
-4时,任取x∈[1,9]恒有f(x-4)-x=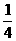 (x2-10x+9)=
(x2-10x+9)=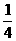 (x-1)(x-9)≤0
(x-1)(x-9)≤0
∴ mmin=9
点评:本题属于存在性探索问题,处理这道题的方法就是通过x的特殊值得出t的大致范围,然后根据t的范围,再对x取特殊值,从而解决问题。
(4)联想类比
例8.在平面几何里,有勾股定理:“设△ABC的两边AB,AC互相垂直,则AB2+AC2=BC2”拓展到空间,类比平面几何的勾股定理,研究三棱锥的侧面面积与底面面积间的关系,可以得出的正确结论是:“设三棱锥A-BCD的三个侧面ABC、ACD、ADB两两相互垂直,则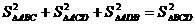 .”
.”
例9.若数列{an}是等差数列,数列{bn}满足bn=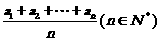 ,则{bn}也为等差数列.类比上述性质,相应地,若数列{cn}是等比数列,且cn>0,数列{dn}满足dn= ,则数列{dn}也为等比数列. 答案:dn=
,则{bn}也为等差数列.类比上述性质,相应地,若数列{cn}是等比数列,且cn>0,数列{dn}满足dn= ,则数列{dn}也为等比数列. 答案:dn=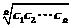 (n∈N*)
(n∈N*)
例10.(2003年上海市春季高考题)设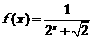 ,利用课本中推导等差数列前n项和的公式的方法,可求得
,利用课本中推导等差数列前n项和的公式的方法,可求得 的值是
的值是
分析:利用f(1-x)+f(x)=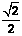 ,可求
,可求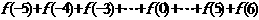 =
=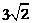
(5)赋值推断
例11.(2004年高考上海卷16)某地2004年第一季度应聘和招聘人数排行榜前5个行业的情况列表如下
|
行业名称 |
计算机 |
机械 |
营销 |
物流 |
贸易 |
|
应聘人数 |
215830 |
200250 |
154676 |
74570 |
65280 |
|
行业名称 |
计算机 |
营销 |
机械 |
建筑 |
化工 |
|
招聘人数 |
124620 |
102935 |
89115 |
76516 |
70436 |
若用同一行业中应聘人数与招聘人数比值的大小来衡量该行业的就业情况,则根据表中数据,就业形势一定是( B )
A.计算机行业好于化工行业 B.建筑行业好于物流行业.
C.机械行业最紧张. D.营销行业比贸易行业紧张
例12.(2004年高考江苏卷)二次函数y=ax2+bx+c(x∈R)的部分对应值如下表:
|
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
|
y |
6 |
0 |
-4 |
-6 |
-6 |
-4 |
0 |
6 |
则不等式ax2+bx+c>0的解集是 .
.
(6)几何意义法
几何意义法就是利用探索性问题的题设所给的数或式的几何意义去探索结论,由于数学语言的抽象性,有些探索性问题的题设表述不易理解,在解题时若能积极地考虑题设中数或式的几何意义所体现的内在联系,巧妙地转换思维角度,将有利于问题的解决。
例13.设x、y为实数,集合A={(x,y)|y2―x―1=0},B={{(x,y)|16x2+8x―2y+5=0},
C={(x,y)|y=kx+b},问是否存在自然数k,b使(A∪B)∩C=φ?
分析:此题等价于是否存在自然数k,b,使得直线y=kx+b与抛物线y2―x―1=0和16x2+8x―2y+5=0都没有交点。
解:因为抛物线y2―x―1=0和16x2+8x―2y+5=0在y轴上的截距分别为1、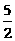 ,所以取b=2,由
,所以取b=2,由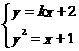 无实数解,得
无实数解,得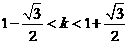 ,从而k=1,
,从而k=1,
此时方程组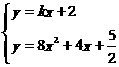 无实数解.故存在k=1,b=2满足(A∪B)∩C=φ.
无实数解.故存在k=1,b=2满足(A∪B)∩C=φ.
点评:与集合运算有关的一类探索性问题,它的题设往往都具有鲜明的几何意义。
 ⑶如果给出的是一块任意三角形的纸片(如图3),要求剪拼成一个直三棱柱模型,使它的全面积与给出的三角形的面积相等,请设计一种剪拼方法,用虚线标示在图3中,并作简要说明.
⑶如果给出的是一块任意三角形的纸片(如图3),要求剪拼成一个直三棱柱模型,使它的全面积与给出的三角形的面积相等,请设计一种剪拼方法,用虚线标示在图3中,并作简要说明.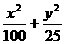 =1,n=3. 点P1(3,0) 及S3=255, 求点P3的坐标;(只需写出一个)
=1,n=3. 点P1(3,0) 及S3=255, 求点P3的坐标;(只需写出一个)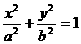 (a>b>0). 点P1(a,0), 对于给定的自然数n, 当公差d变化时, 求Sn的最小值;
(a>b>0). 点P1(a,0), 对于给定的自然数n, 当公差d变化时, 求Sn的最小值;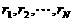 的大小关系,并指出除第N组外的每组至少含有几个数
的大小关系,并指出除第N组外的每组至少含有几个数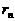 的大小关系,并证明
的大小关系,并证明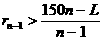
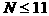
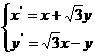 看作坐标平面内的一个变换,它将平面内的点P变换到这一平面上的Q点。是否存在这样的直线它上面的任何一点经过上述变换后得到的点仍旧在该直线上。若存在,求出所有这样的直线;若不存在,说明理由。
18.(本小题满分12分)已知f(x)=
看作坐标平面内的一个变换,它将平面内的点P变换到这一平面上的Q点。是否存在这样的直线它上面的任何一点经过上述变换后得到的点仍旧在该直线上。若存在,求出所有这样的直线;若不存在,说明理由。
18.(本小题满分12分)已知f(x)=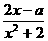 (x∈R)在区间[-1,1]上是增函数.
(x∈R)在区间[-1,1]上是增函数.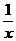 的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.
的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.