3.(2005年黄冈市调研题)如果方程 +
+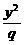 =1表示双曲线,则下列椭圆中,与该双曲线共焦点的是
=1表示双曲线,则下列椭圆中,与该双曲线共焦点的是
A.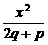 +
+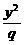 =1
B.
=1
B.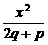 +
+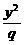 =-1
=-1
C.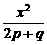 +
+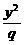 =1
D.
=1
D.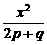 +
+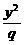 =-1
=-1
解析:由题意有pq>0,若p>0,q>0,则双曲线焦点位于y轴上且c2=p+q无答案,则只有p<0,q<0,焦点位于x轴上,且c2=-p-q,B答案符合.
答案:B
|
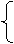 x=2cosθ,
x=2cosθ,
y=sinθ(其中参数θ∈R)上的点的最短距离为
A.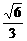 B.1
C.
B.1
C. 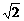 D.
D. 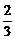
解析:d=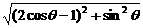
=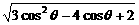
=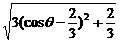 ,
,
dmin=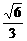 .
.
答案:A
21.(12分)已知四棱锥P-ABCD中,PA⊥面ABCD,底面ABCD为菱形,∠BAD=60°,AB=2,PA=4,E为PC的中点.
(1)求证:平面BDE⊥平面ABCD;
(2)求二面角B-DE-C的大小.
(1)证明:设AC∩BD=O,连结OE.
∵E为PC的中点,O为AC的中点.
∴EO∥PA.
∵PA⊥面ABCD,∴EO⊥面ABCD.
∵EO 平面BDE,∴面BDE⊥面ABCD.
平面BDE,∴面BDE⊥面ABCD.
(2)解法一:过O作OF⊥DE于F,连结CF.
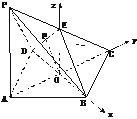
由(1)可知OC⊥面BDE,
∴DE⊥FC.
∴∠OFC为B-DE-C的平面角.
∵OE=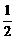 PA=2,OD=1,∴OF=
PA=2,OD=1,∴OF=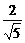 .
.
又∵OC= ,∴tan∠OFC=
,∴tan∠OFC=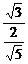 =
=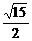 .
.
∴二面角B-DE-C的大小为arctan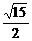 .
.
解法二:以O为原点建立如上图所示的坐标系,则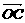 为平面EBD的法向量,
为平面EBD的法向量,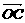 =(0,
=(0, ,0).
,0).
设平面CDE的法向量n=(x,y,z).
∵E(0,0,2),C(0, ,0),D(-1,0,0),
,0),D(-1,0,0),
∴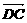 =(1,
=(1, ,0),
,0),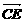 =(0,-
=(0,- ,2).
,2).
∵n·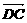 =0,n·
=0,n·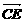 =0,
=0,
|
|
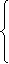
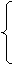 x+
x+ y=0, x=-
y=0, x=- y,
y,
- y+2z=0. z=
y+2z=0. z=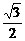 y.
y.
取y= ,则n=(-3,
,则n=(-3, ,
,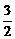 ).∴cos〈n,
).∴cos〈n,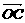 〉=
〉=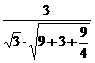 =
=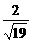 .
.
∴二面角B-DE-C的大小为arccos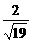 .
.
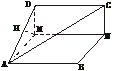
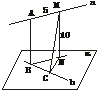
20.(12分)(理)如图,已知矩形ABCD,PA⊥平面ABCD,M、N分别是AB、PC的中点,设AB=a,BC=b,PA=c.
(1)建立适当的空间直角坐标系,写出A、B、M、N点的坐标,并证明MN⊥AB;
(2)平面PDC和平面ABCD所成的二面角为θ,当θ为何值时(与a、b、c无关),MN是直线AB和PC的公垂线段.
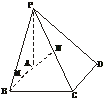
(1)证明:以A为原点,分别以AB、AD、AP为x轴、y轴、z轴,建立空间直角坐标系.
则A(0,0,0),B(a,0,0),M( ,0,0),N(
,0,0),N( ,
,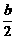 ,
,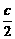 ).
).
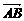 =(a,0,0),
=(a,0,0),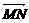 =(0,
=(0,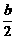 ,
,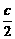 ).
).
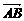 ·
·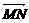 =0
=0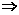 AB⊥MN.
AB⊥MN.
(2)解:P(0,0,c),C(a,b,0),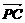 =(a,b,-c),若MN是PC、AB的公垂线段,则
=(a,b,-c),若MN是PC、AB的公垂线段,则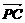 ·
·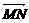 =0,即-
=0,即-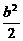 +
+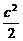 =0
=0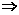 b=c.
b=c.
|
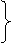 又∵AP⊥面ABCD
又∵AP⊥面ABCD
CD⊥DA
∴∠PDA是二面角P-CD-A的平面角.
∴∠PDA=45°,
即二面角P-CD-A是45°.
(文)正方体ABCD-A1B1C1D1中,M、N、P分别为棱AB、BC、DD1的中点.
(1)求证:PB⊥平面MNB1;
(2)设二面角M-B1N-B为α,求cosα的值.
(1)证明:如图,以D为原点,DA、DC、DD1分别为x轴、y轴、z轴建立空间直角坐标系,取正方体棱长为2,则P(0,0,1)、M(2,1,0)、B(2,2,0)、B1(2,2,2).
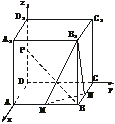
∵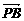 ·
·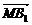 =(2,2,-1)·(0,1,2)=0,
=(2,2,-1)·(0,1,2)=0,
∴MB1⊥PB,同理,知NB1⊥PB.
∵MB1∩NB1=B1,∴PB⊥平面MNB1.
(2)∵PB⊥平面MNB1,BA⊥平面B1BN,∴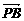 =(2,2,-1)与
=(2,2,-1)与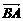 =(0,2,0)所夹的角即为α,cosα=
=(0,2,0)所夹的角即为α,cosα=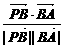 =
=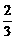 .
.
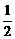 D.-
D.- ,k2=
,k2=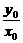 =
= .
.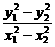 =-
=-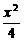 -
-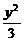 =-1交于两点,则直线l的斜率的取值范围是
=-1交于两点,则直线l的斜率的取值范围是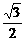 ,
,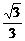 ,
,
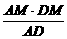 =
=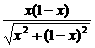 (0<x<1).
(0<x<1).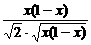 =
=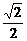
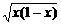 ≤
≤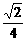 ,当且仅当x=1-x,即x=
,当且仅当x=1-x,即x=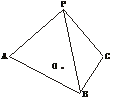
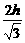 .
.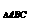 =
=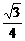 (4h)2=4
(4h)2=4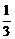 ·4
·4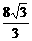 h3,∴h=3,
h3,∴h=3,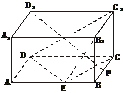
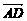 、
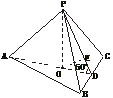
、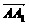 分别为x轴、y轴、z轴的正向建立空间直角坐标系,则有D(0,3,0)、D1(0,3,2)、E(3,0,0)、F(4,1,0)、C1(4,3,2).
分别为x轴、y轴、z轴的正向建立空间直角坐标系,则有D(0,3,0)、D1(0,3,2)、E(3,0,0)、F(4,1,0)、C1(4,3,2).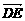 =(3,-3,0),
=(3,-3,0),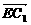 =(1,3,2),
=(1,3,2),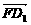 =(-4,2,2).
=(-4,2,2).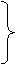


 设向量n=(x,y,z)与平面C1DE垂直,则有 n⊥
设向量n=(x,y,z)与平面C1DE垂直,则有 n⊥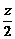 ,-
,-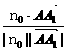 =
=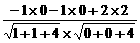 =
=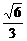 .
. =
=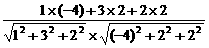 =
=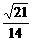 .
.
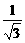 BD=2.
BD=2. ABCD·BB1=8
ABCD·BB1=8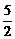
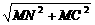 =
=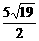 .
.