12.关于方程x2+2y2-ax+ay-a-1=0(a∈R)表示的椭圆,给出以下四个命题:
①椭圆的中心在一条直线上运动;
②椭圆的大小不变;
③不论a取什么值,椭圆总过两个定点;
④椭圆的离心率不变.
其中错误命题的个数是
A.3 B.2 C.1 D.0
解析:椭圆方程为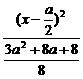 +
+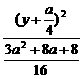 =1,
=1,
故中心(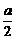 ,-
,-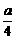 )在直线y=-
)在直线y=-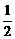 x上运动.
x上运动.
∴①成立.
离心率e=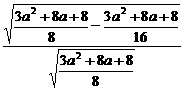 =
=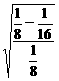 =
=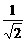 (定值),故④成立.
(定值),故④成立.
随a的变化,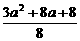 与
与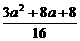 均变化,故②不成立.
均变化,故②不成立.
椭圆方程又可写为(x2+2y2-1)+a(-x+y-1)=0.
|
|
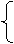 x2+2y2-1=0,
x2+2y2-1=0,
-x+y-1=0,
由Δ=42-4×3>0知方程组有两组解,故③成立.
综上知只有②错误,故选C.
答案:C
 =-
=-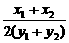 =-
=-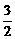 .代入x2+2y2=4,
.代入x2+2y2=4,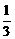 .
.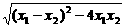 ·
·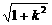 =
=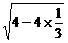 ·
·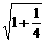 =
=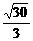 .
.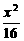 -
-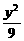 =1的右顶点为顶点,左焦点为焦点的抛物线的方程是____________.
=1的右顶点为顶点,左焦点为焦点的抛物线的方程是____________.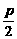 =4-(-5),∴p=18.
=4-(-5),∴p=18.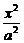 -
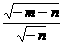
-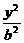 =1(a>0,b>0)右支上一点,F1、F2分别是左、右焦点,且焦距为2c,则△PF1F2的内切圆圆心的横坐标为
=1(a>0,b>0)右支上一点,F1、F2分别是左、右焦点,且焦距为2c,则△PF1F2的内切圆圆心的横坐标为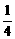 =0
=0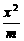 -
-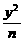 =1(mn≠0)的离心率为2,则
=1(mn≠0)的离心率为2,则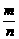 的值为
的值为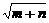 ,a=
,a= ,由题意
,由题意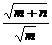 =2,解得
=2,解得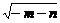 =,a=
=,a=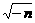 ,
, =2,解得
=2,解得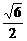 ,F1、F2分别是它的左、右焦点,若过F1的直线与双曲线的左支交于A、B两点,且|AB|是|AF2|与|BF2|的等差中项,则|AB|等于
,F1、F2分别是它的左、右焦点,若过F1的直线与双曲线的左支交于A、B两点,且|AB|是|AF2|与|BF2|的等差中项,则|AB|等于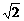 B.4
B.4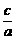 =
=