13.(2005年北京东城区目标检测题)设实数x、y满足
|
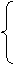 x≥0,
x≥0,
x-y+2≤0,
2x+y-5≤0,
解析:画出图形即可得到在(0,5)点z=x+y取得最大值5.
答案:5
12.(2002年全国新课程)平面直角坐标系中,O为坐标原点,已知两点A(3,1)、
B(-1,3),若点C满足 =α
=α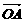 +β
+β ,其中α、β∈R,且α+β=1,则点C的轨迹方程为
,其中α、β∈R,且α+β=1,则点C的轨迹方程为
A.(x-1)2+(y-2)2=5
B.3x+2y-11=0
C.2x-y=0
D.x+2y-5=0
解析:设C点坐标为(x,y),则 =(x,y),
=(x,y),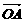 =(3,1),
=(3,1), =(-1,3),
=(-1,3),
所以(x,y)=α·(3,1)+β·(-1,3)=(3α-β,α+3β).
|
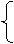 x=3α-β,
x=3α-β,
y=α+3β,
|
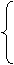 α=
α=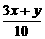 ,
,
β=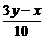 .
.
因为α+β=1,
所以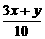 +
+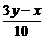 =1,即x+2y-5=0.故选D.
=1,即x+2y-5=0.故选D.
答案:D
11.如果直线y=kx+1与圆x2+y2+kx+my-4=0交于M、N两点,且M、N关于直线x+y=0对称,则不等式组
|
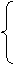 kx-y+1≥0,
kx-y+1≥0,
kx-my≤0,
y≥0
A. B.
B.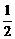 C.1
D.2
C.1
D.2
解析:由题中条件知k=1,m=-1,易知区域面积为 .
.
答案:A
9.圆x2+y2+2x+4y-3=0上到直线x+y+1=0的距离为 的点共有
的点共有
A.1个 B.2个 C.3个 D.4个
解析:易知圆心(-1,-2)到x+y+1=0的距离d= ,所以满足题意的点共有3个.
,所以满足题意的点共有3个.
答案:C
|
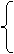 x=1+cosθ,
x=1+cosθ,
y=1-sinθ (θ为参数),直线l经过点(0, ),倾斜角为α,则α=
),倾斜角为α,则α=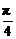 是直线l与曲线C相切的
是直线l与曲线C相切的
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
解析:数形结合法易知.
答案:A
6.(2004年天津,理7)若P(2,-1)为圆(x-1)2+y2=25的弦AB的中点,则直线AB的方程是
A.x-y-3=0 B.2x+y-3=0
C.x+y-1=0 D.2x-y-5=0
解:由(x-1)2+y2=25知圆心为Q(1,0).据kQP·kAB=-1,
∴kAB=- =1(其中kQP=
=1(其中kQP=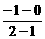 =-1).
=-1).
∴AB的方程为y=(x-2)-1=x-3,即x-y-3=0.
答案:A
|
|
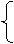 x=3+5cosθ,
x=3+5cosθ,
y=-4+5sinθ
A.10 B.16 C.25 D.100
解析:易知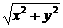 是圆(x-3)2+(y+4)2=25上的点到原点的距离.
是圆(x-3)2+(y+4)2=25上的点到原点的距离.
答案:D
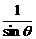 ,k2=-2sinθ.
,k2=-2sinθ.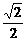 ,
,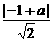 .
. +
+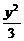 =1的公共点有____________个.
=1的公共点有____________个.