22.(14分)过点A(0,a)作直线与圆E:(x-2)2+y2=1交于B、C两点,在BC上取满足BP∶PC=AB∶AC的点P.
(1)求P点的轨迹方程;
(2)设所求轨迹方程与圆E交于M、N两点,求△EMN(E为圆心)面积的最大值.
解:(1)设AB方程为y=kx+a,与圆的方程联立得(k2+1)x2+(2ak-4)x+a2+3=0.
xB+xC=-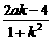 ,xB·xC=
,xB·xC=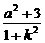 .
.
∵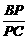 =
=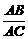 ,∴
,∴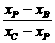 =
=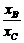 .
.
∴xP=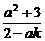 .
.
同理,yP=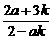 .
.
消去k,得2x-ay-3=0.
∴轨迹是直线2x-ay-3=0在圆内一段.
|
|
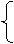 2x-ay-3=0
2x-ay-3=0
(x-2)2+y2=1
|MN|=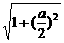 |y1-y2|=2·
|y1-y2|=2·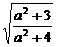 .
.
又高为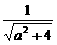 ,∴S△EMN=
,∴S△EMN=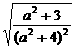 =
=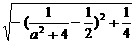 ≤
≤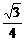 .
.
仅当a=0时,(S△EMN)max=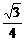 .
.
20.(12分)某房产开发公司建楼急需资金1200万元,必须向银行A和银行B贷款,一年本自息还清,银行A至多贷给该公司800万元,年息12%;银行B至多贷款给该公司1000万元,年息14%,问开发公司分别向A、B两银行贷款多少万元,才使所付总利息最少?
解:设开发公司向银行A贷款x万元,向银行B贷款y万元,开发公司需付总利息为S,依题意,有约束条件
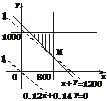
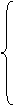 x≤800,
x≤800,
|
x+y≥1200,
x≥0,
y≥0.
作出以上不等式组所表示的平面区域,即可行域.作直线l0:0.12x+0.14y=0,把直线l0向右上方平移至l1的位置时,直线经过可行域上的点M,且与原点距离最小,此时,S=0.12x+0.14y取得最小值.
|
|
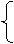 x=800,
x=800,
x+y=1200,
故该开发公司向银行A贷款800万元,向银行B贷款400万元时,所付总利息最少.
19.(12分)圆C通过不同的三点P(k,0)、Q(2,0)、R(0,1),已知圆C在P点切线斜率为1,试求圆C的方程.
解:设圆C的方程为x2+y2+Dx+Ey+F=0.
|
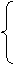 k+2=-D,
k+2=-D,
2k=F,
E+F+1=0.
∴圆的方程为x2+y2-(k+2)x-(2k+1)y+2k=0,圆心为(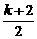 ,
, ).
).
又∵kCP=-1,∴k=-3.
∴圆的方程为x2+y2+x+5y-6=0.
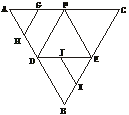
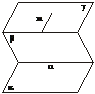
 FD,GH
FD,GH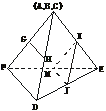
 α或n∥α
α或n∥α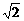 、
、 、
、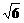 ,这个长方体对角线的长为
,这个长方体对角线的长为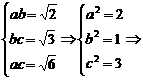 l=
l=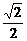 B.
B.
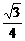 D.
D.
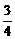
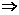 (a2+4)y2-2ay+3=0.
(a2+4)y2-2ay+3=0. |=
|= .
. )2+
)2+ >0成立.
>0成立.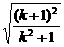 =
= ≤
≤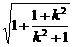 =
= .
.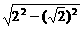 =2
=2
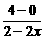 ,kPB=
,kPB=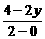 (x≠1),
(x≠1),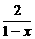 ·
·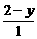 =-1(x≠1).
=-1(x≠1).
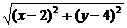 ,|AB|=
,|AB|=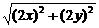 ,
,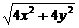 .化简,得x+2y-5=0,为所求轨迹方程.
.化简,得x+2y-5=0,为所求轨迹方程.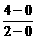 =2,线段OP的中点为(1,2),
=2,线段OP的中点为(1,2),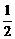 (x-1),即x+2y-5=0为所求.
(x-1),即x+2y-5=0为所求.