0 50399 50407 50413 50417 50423 50425 50429 50435 50437 50443 50449 50453 50455 50459 50465 50467 50473 50477 50479 50483 50485 50489 50491 50493 50494 50495 50497 50498 50499 50501 50503 50507 50509 50513 50515 50519 50525 50527 50533 50537 50539 50543 50549 50555 50557 50563 50567 50569 50575 50579 50585 50593 447348
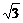 ,则
,则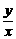 的最大值是
的最大值是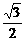 B.
B.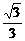 C.
C.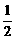 D.
D.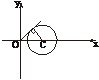
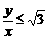 .
.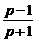 为纯虚数,则与复数p对应的点P
为纯虚数,则与复数p对应的点P 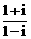 )n+(
)n+(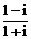 )n(n∈Z),则集合{x|x=f(n)}中元素的个数是
)n(n∈Z),则集合{x|x=f(n)}中元素的个数是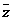 ∈R;
∈R;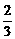 <m<1时,复数z=(3m-2)+(m-1)i在复平面上对应的点位于
<m<1时,复数z=(3m-2)+(m-1)i在复平面上对应的点位于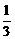 <m-1<0.
<m-1<0.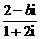 (其中i为虚数单位,b为实数)的实部和虚部互为相反数,那么b等于
(其中i为虚数单位,b为实数)的实部和虚部互为相反数,那么b等于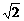 B.
B.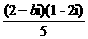 =
=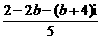
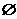 ,求a的取值范围.
,求a的取值范围.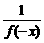 >1.
>1.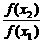 <1.∴f(x2)<f(x1).
<1.∴f(x2)<f(x1).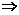 f(x2+y2)>f(1).
f(x2+y2)>f(1).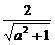 ≥1
≥1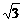 ≤a≤
≤a≤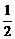 ],都有f(x1+x2)=f(x1)·f(x2).
],都有f(x1+x2)=f(x1)·f(x2).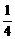 );
);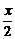 )·f(
)·f(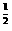 .
.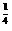 .
. f(x)=
f(x)=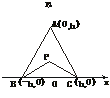
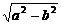 ,设P的坐标为(0,y),则P至三镇距离的平方和为
,设P的坐标为(0,y),则P至三镇距离的平方和为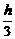 )2+
)2+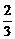 h2+2b2.
h2+2b2.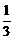
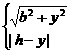
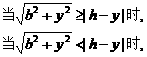
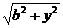 ≥|h-y|解得y≥
≥|h-y|解得y≥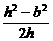 ,记y*=
,记y*=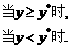
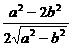 );
);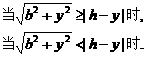
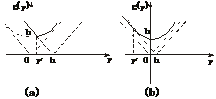
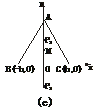
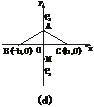
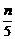 ,yn=
,yn=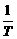 (a0+a1+…+an),作函数y=f(x),使其图象为逐点依次连结点Pn(xn,yn)(n=0,1,2,…,5)的折线.
(a0+a1+…+an),作函数y=f(x),使其图象为逐点依次连结点Pn(xn,yn)(n=0,1,2,…,5)的折线.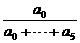 =0,
=0,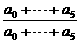 =1.
=1.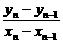 =
=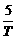 an,n=1,2,…,5.
an,n=1,2,…,5.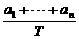 <
<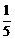 (k1+k2+…+kn)<
(k1+k2+…+kn)<