0 50381 50389 50395 50399 50405 50407 50411 50417 50419 50425 50431 50435 50437 50441 50447 50449 50455 50459 50461 50465 50467 50471 50473 50475 50476 50477 50479 50480 50481 50483 50485 50489 50491 50495 50497 50501 50507 50509 50515 50519 50521 50525 50531 50537 50539 50545 50549 50551 50557 50561 50567 50575 447348
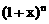 的展开式中,若第三项与第六项的系数相等,则
的展开式中,若第三项与第六项的系数相等,则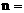 _____。[7]
_____。[7]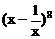 的展开式中,
的展开式中,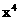 的系数与
的系数与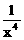 的系数之差是_________。[0]
的系数之差是_________。[0]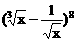 的展开式中,x的一次项的系数是___________。[28]
的展开式中,x的一次项的系数是___________。[28]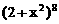 的展开式中
的展开式中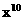 的系数。[448]
的系数。[448]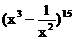 的展开式中的常数项。[-5005]
的展开式中的常数项。[-5005]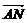 、
、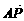 =6|
=6|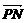 |,
|,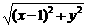 ,
,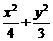 =1. 4分
=1. 4分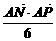 =-
=- (x-4).
(x-4).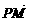 |=m,|
|=m,|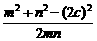
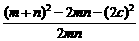 =
=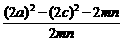
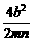 -1=
-1=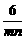 -1≥
-1≥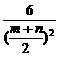 -1=
-1=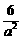 -1=
-1=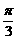 ]. 14分
]. 14分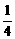 an,bn+1=bn(1-
an,bn+1=bn(1-
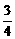 .
.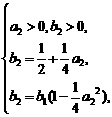
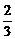 ,b2=
,b2=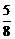 和a4=
和a4=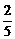 ,b4=
,b4=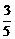 ,
,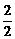 ,a2=
,a2=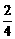 ,a4=
,a4=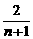 (n∈N*).④
(n∈N*).④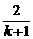 .
.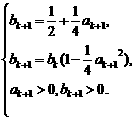
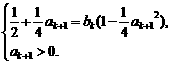 ⑤
⑤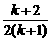 ,把它代入⑤式解得
,把它代入⑤式解得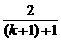 ,
,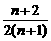 .
.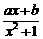 在x=2处有一个极大值.
在x=2处有一个极大值.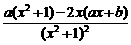 =
=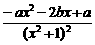 . ①
. ①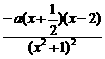 .
.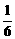 ;并证明如果P=
;并证明如果P=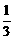 (P1+P2+…+P6)+
(P1+P2+…+P6)+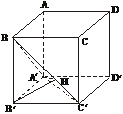
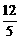 ,
,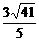 .
.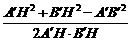 =
=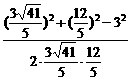 =
=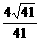 .
.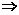
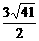 ·d=
·d=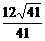 为所求. 12分
为所求. 12分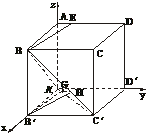
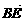 =(0,t,4)-(3,0,4)=(-3,t,0).
=(0,t,4)-(3,0,4)=(-3,t,0).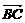 =
=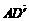 =
=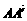 +
+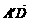 =(0,0,-4)+(0,3,0)=(0,3,-4),
=(0,0,-4)+(0,3,0)=(0,3,-4),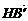 =(0,-y,-z).
=(0,-y,-z).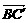 =(3,3,0)-(3,0,4)=(0,3,-4),
=(3,3,0)-(3,0,4)=(0,3,-4),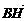 =λ
=λ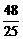 ,z=
,z=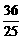 .
.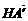 =(-3,-
=(-3,-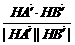
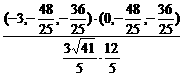
 平面A′BC′,
平面A′BC′,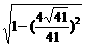 =
=