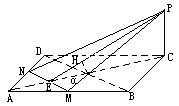
摘要:如图.ABCD是边长为1的正方形.M.N分别是DA.BC上的点.且MN∥AB.现沿MN折成直二面角AB-MN-CD. (1)求证:平面ADC⊥平面AMD, (2)设AM=x(0<x<1).MN到平面ADC的距离为y.试用x表示y, (3)点M在什么位置时.y有最大值.最大值为多少? (1)证明:∵ABCD是正方形.且MN∥AB∥CD.∴MN⊥AM.MN⊥DM.即CD⊥AM.CD⊥DM.∴CD⊥平面AMD. ∵CD平面ADC. ∴平面ADC⊥平面AMD. (2)解:∵MN∥CD.∴MN∥平面ADC.故MN到平面ADC的距离即为M到平面ADC的距离.过M作MH⊥AD于H.∵平面ADC⊥平面AMD. ∴MH⊥平面ADC.即MH为所求距离. 在Rt△AMD中.求得y==(0<x<1). (3)解:y≤=≤.当且仅当x=1-x.即x=时.ymax=.此时M为AD的中点.
网址:http://m.1010jiajiao.com/timu3_id_504857[举报]
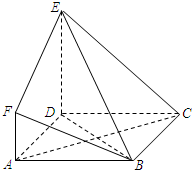
 如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.
如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.(1)求证:AC⊥平面BDE;
(2)设点M是线段BD 上一个动点,试确定点M的位置,使得AM∥平面BEF,并证明你的结论.
如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成的角为60°. 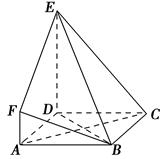
(1)求证:AC⊥平面BDE;
(2)求二面角F-BE-D的余弦值;
(3)设点M是线段BD上一个动点,试确定点M的位置,使得AM∥平面BEF,并证明你的结论.