0 45885 45893 45899 45903 45909 45911 45915 45921 45923 45929 45935 45939 45941 45945 45951 45953 45959 45963 45965 45969 45971 45975 45977 45979 45980 45981 45983 45984 45985 45987 45989 45993 45995 45999 46001 46005 46011 46013 46019 46023 46025 46029 46035 46041 46043 46049 46053 46055 46061 46065 46071 46079 447348
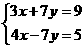 的解是 ( )D
的解是 ( )D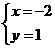 B.
B.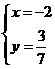 C.
C.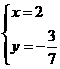 D.
D.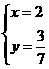
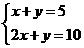 ,由②
,由② ①,得正确的方程是( )B
①,得正确的方程是( )B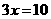 B.
B. 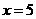 C.
C. 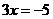 D.
D. 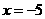
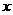 元,则所列方程正确的是( )C
元,则所列方程正确的是( )C
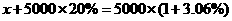
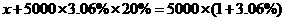
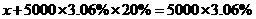
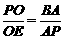 .即
.即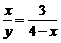 .∴y=
.∴y=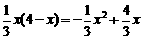 (0<x<4).
(0<x<4).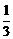 .………………………………………………………………4分
.………………………………………………………………4分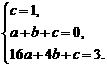 ∴
∴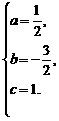
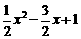 .……………………………………………………………………………8分
.……………………………………………………………………………8分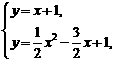 得
得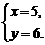 ∴Q(5,6).
∴Q(5,6).
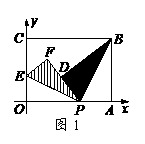
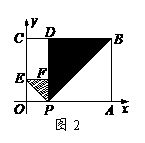
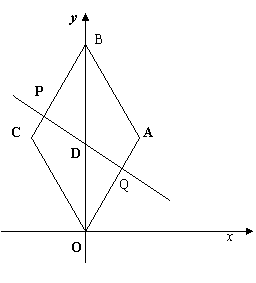 (湖北黄岗)已知:如图,在平面直角坐标系中,四边形ABCO是菱形,且∠AOC=60°,点B的坐标是
(湖北黄岗)已知:如图,在平面直角坐标系中,四边形ABCO是菱形,且∠AOC=60°,点B的坐标是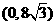 ,点P从点C开始以每秒1个单位长度的速度在线段CB上向点B移动,设
,点P从点C开始以每秒1个单位长度的速度在线段CB上向点B移动,设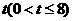 秒后,直线PQ交OB于点D.
秒后,直线PQ交OB于点D.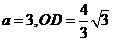 时,求t的值及此时直线PQ的解析式;
时,求t的值及此时直线PQ的解析式;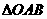 相似?当a 为何值时,以O,P,Q,D为顶点的三角形与
相似?当a 为何值时,以O,P,Q,D为顶点的三角形与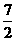 的抛物线经过点A(6,0)和B(0,4).
的抛物线经过点A(6,0)和B(0,4).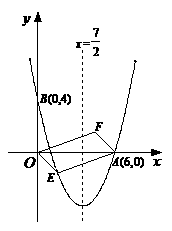
 的扇形.
的扇形.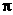 ).(3分)
).(3分) 的半径
的半径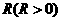 为任意值时,(2)中的结论是否仍然成立?请说明理由.(5分)
为任意值时,(2)中的结论是否仍然成立?请说明理由.(5分)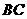 ,由勾股定理求得:
,由勾股定理求得: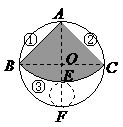
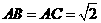 ·································································· 1分
·································································· 1分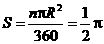 ································································· 2分
································································· 2分 并延长,与弧
并延长,与弧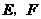 ,
,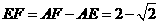 ····························································································· 1分
····························································································· 1分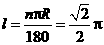 ······················································································ 2分
······················································································ 2分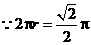
 圆锥的底面直径为:
圆锥的底面直径为: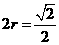 ··················································································· 3分
··················································································· 3分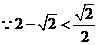 ,
,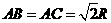
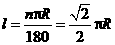 ···················································································· 1分
···················································································· 1分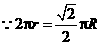
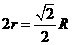 ················································································ 2分
················································································ 2分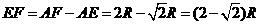
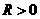
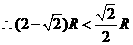 ···································································································· 3分
···································································································· 3分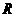 为何值,
为何值,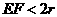 ··················································································· 4分
··················································································· 4分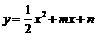 交
交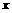 轴于A、B两点,交
轴于A、B两点,交 轴于点C,点P是它的
轴于点C,点P是它的
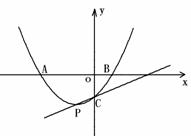 顶点,点A的横坐标是
顶点,点A的横坐标是 3,点B的横坐标是1.
3,点B的横坐标是1. 、
、 的值;
的值;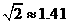 ,
,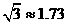 ,
,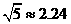 )
)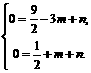 ……………………………………2分
……………………………………2分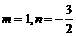 .
………………………3分
.
………………………3分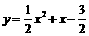 , ∴ P(-1,-2),C
, ∴ P(-1,-2),C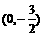 . …………………4分
. …………………4分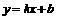 ,则
,则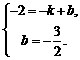 解得
解得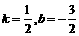 .
. 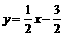 .
…………………………6分
.
…………………………6分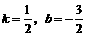 ,不写最后一步,不扣分.
,不写最后一步,不扣分.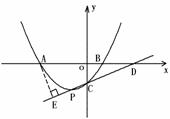 设直线PC与
设直线PC与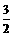 ,
,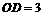 ,
,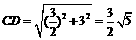 .
…………8分
.
…………8分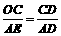 , 即
, 即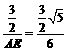 . ∴
. ∴ 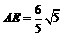 . …………………11分
. …………………11分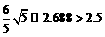 ,
,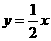 与双曲线
与双曲线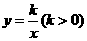 交于
交于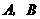 两点,且点
两点,且点 的横坐标为
的横坐标为 .
. 的值;
的值; 的纵坐标为8,求
的纵坐标为8,求 的面积;
的面积;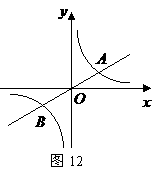 (3)过原点
(3)过原点 的另一条直线
的另一条直线 交双曲线
交双曲线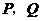 两点(
两点(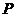 点在第一象限),若由点
点在第一象限),若由点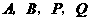 为顶点组成的四边形面积为
为顶点组成的四边形面积为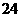 ,求点
,求点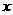 = 4时,
= 4时,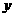 = 2 .
= 2 .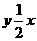 与双曲线
与双曲线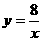 (k>0)的交点 ,
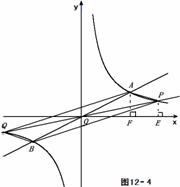
(k>0)的交点 ,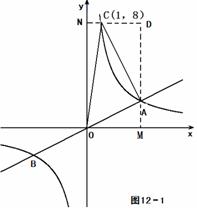 (2) 解法一:如图12-1,
(2) 解法一:如图12-1, 上,当
上,当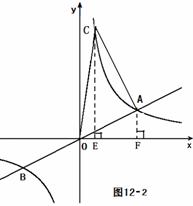 过点
C、A分别做
过点
C、A分别做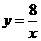 上,当
上,当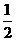 ×(2+8)×3 = 15 ,
×(2+8)×3 = 15 , 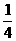 ∴ 四边形APBQ是平行四边形 .
∴ 四边形APBQ是平行四边形 .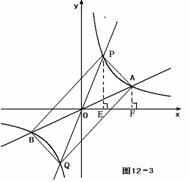
 (
(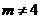 ),
),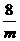 得P (
得P ( 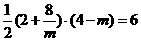 .
. ∴ P(2,4).
∴ P(2,4).
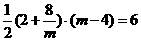 ,
,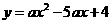 经过
经过 的三个顶点,已知
的三个顶点,已知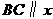 轴,点
轴,点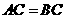 .
.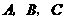 三点的坐标并求抛物线的解析式;
三点的坐标并求抛物线的解析式;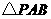 是等腰三角形.若存在,求出所有符合条件的点
是等腰三角形.若存在,求出所有符合条件的点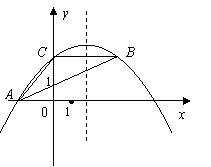
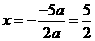 ………2分
………2分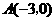
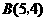
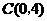 …………5分
…………5分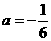 ………6分
………6分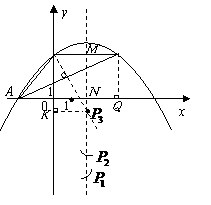
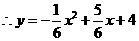 …………………………………………7分
…………………………………………7分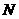 ,与
,与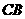 交于
交于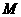 .
.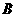 作
作 轴于
轴于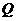 ,易得
,易得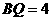 ,
,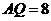 ,
,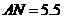 ,
,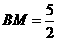
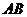 为腰且顶角为角
为腰且顶角为角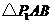 .
.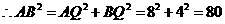 ······································································ 8分
······································································ 8分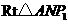 中,
中,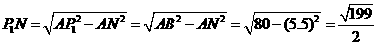
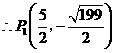 ································································································· 9分
································································································· 9分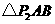 .
.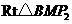 中,
中,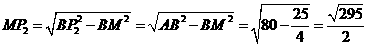 ···· 10分
···· 10分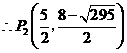 ····························································································· 11分
····························································································· 11分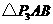 .
.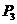 ,此时平分线必过等腰
,此时平分线必过等腰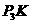 垂直
垂直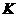 ,显然
,显然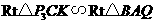 .
.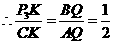 .
.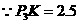
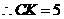 于是
于是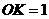 ······························································ 13分
······························································ 13分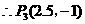 ······································································································· 14分
······································································································· 14分