0 45884 45892 45898 45902 45908 45910 45914 45920 45922 45928 45934 45938 45940 45944 45950 45952 45958 45962 45964 45968 45970 45974 45976 45978 45979 45980 45982 45983 45984 45986 45988 45992 45994 45998 46000 46004 46010 46012 46018 46022 46024 46028 46034 46040 46042 46048 46052 46054 46060 46064 46070 46078 447348
 (常州)已知
(常州)已知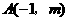 与
与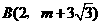 是反比例函数
是反比例函数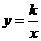 图象上的两个点.
图象上的两个点.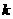 的值;
的值;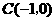 ,则在反比例函数
,则在反比例函数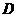 ,使得以
,使得以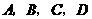 四点为顶点的四边形为梯形?若存在,求出点
四点为顶点的四边形为梯形?若存在,求出点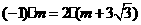 ,得
,得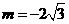 ,因此
,因此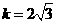 .···························· 2分
.···························· 2分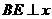 轴,
轴,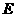 为垂足,则
为垂足,则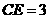 ,
,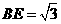 ,
,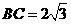 ,因此
,因此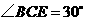 .
.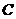 与点
与点 的横坐标相同,因此
的横坐标相同,因此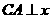 轴,从而
轴,从而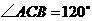 .
. 为底时,由于过点
为底时,由于过点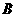 且平行于
且平行于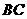 为底时,过点
为底时,过点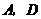 分别作
分别作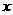 轴,
轴,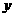 轴的平行线,交于点
轴的平行线,交于点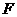 .
.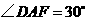 ,设
,设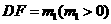 ,则
,则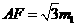 ,
,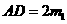 ,
,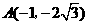 ,得点
,得点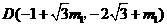 .
.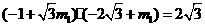 ,
,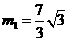 (
(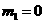 舍去),因此点
舍去),因此点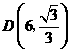 .
.
 此时
此时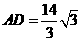 ,与
,与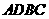 是梯形.······························· 5分
是梯形.······························· 5分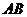 为底时,过点
为底时,过点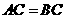 ,因此
,因此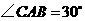 ,从而
,从而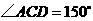 .作
.作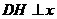 轴,
轴,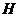 为垂足,
为垂足,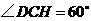 ,设
,设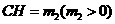 ,则
,则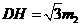 ,
,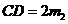
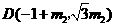 ,
,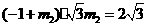 .
.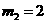 (
(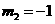 舍去),因此点
舍去),因此点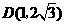 .
.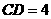 ,与
,与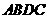 是梯形.··································· 7分
是梯形.··································· 7分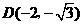 ,四边形
,四边形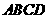 是梯形.··················································· 9分
是梯形.··················································· 9分 综上所述,函数
综上所述,函数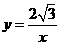 图象上存在点
图象上存在点 (安徽)按右图所示的流程,输入一个数据x,根据y与x的关系式就输出一个数据y,这样可以将一组数据变换成另一组新的数据,要使任意一组都在20-100(含20和100)之间的数据,变换成一组新数据后能满足下列两个要求:
(安徽)按右图所示的流程,输入一个数据x,根据y与x的关系式就输出一个数据y,这样可以将一组数据变换成另一组新的数据,要使任意一组都在20-100(含20和100)之间的数据,变换成一组新数据后能满足下列两个要求: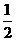 时,这种变换满足上述两个要求;
时,这种变换满足上述两个要求;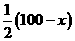 ,即y=
,即y=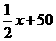 。
。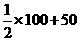 =100。而原数据都在20-100之间,所以新数据都在60-100之间,即满足条件(Ⅰ),综上可知,当P=
=100。而原数据都在20-100之间,所以新数据都在60-100之间,即满足条件(Ⅰ),综上可知,当P=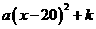 ,……8分
,……8分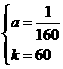 , ∴
, ∴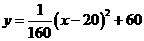 。………14分
。………14分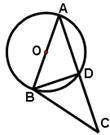
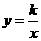
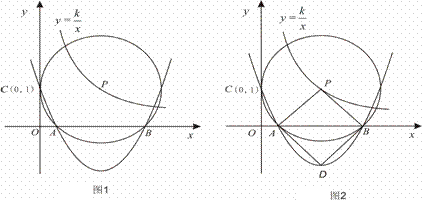
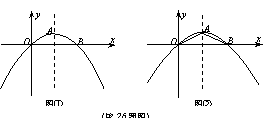
 图象上,并与x轴相交于A、B两点. 且始终与y轴相切于定点C(0,1).
图象上,并与x轴相交于A、B两点. 且始终与y轴相切于定点C(0,1).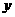 轴相切于点C (0,1),
轴相切于点C (0,1),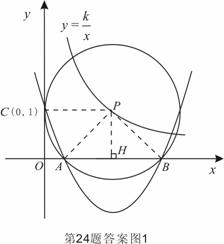
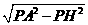 =
=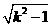 ,
,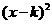 +h. …………………………………………………5分
+h. …………………………………………………5分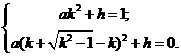
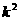 .
…………………7分
.
…………………7分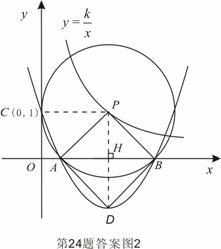
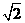 …………………………………………………………11分
…………………………………………………………11分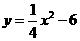 与直线
与直线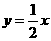 相交于
相交于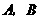 两点.
两点.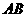 的长.
的长.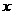 轴、
轴、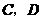 两点,垂足为点
两点,垂足为点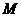 ,分别求出
,分别求出 的长,并验证等式
的长,并验证等式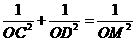 是否成立.
是否成立.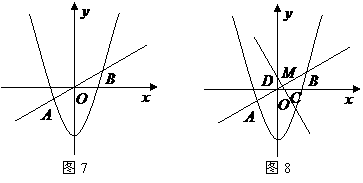
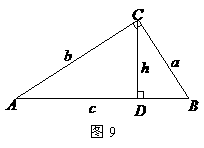 (4)如图9,在
(4)如图9,在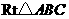 中,
中,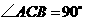 ,
,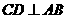 ,垂足为
,垂足为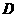 ,设
,设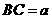 ,
,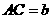 ,
,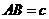 .
.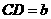 ,试说明:
,试说明: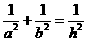 .
.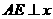 轴,
轴,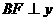 轴,垂足分别为E、F
轴,垂足分别为E、F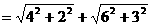
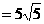
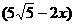 ,扇形的面积为
,扇形的面积为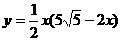
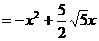
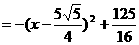
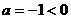
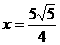 时,函数有最大值
时,函数有最大值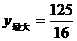
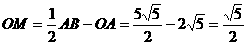
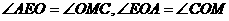
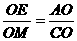 ∴
∴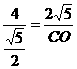 ∴
∴
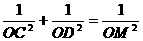
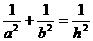 成立.理由如下:
成立.理由如下: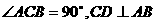
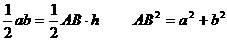
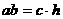
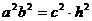
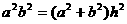
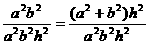
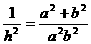
 ∴
∴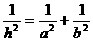
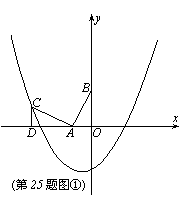
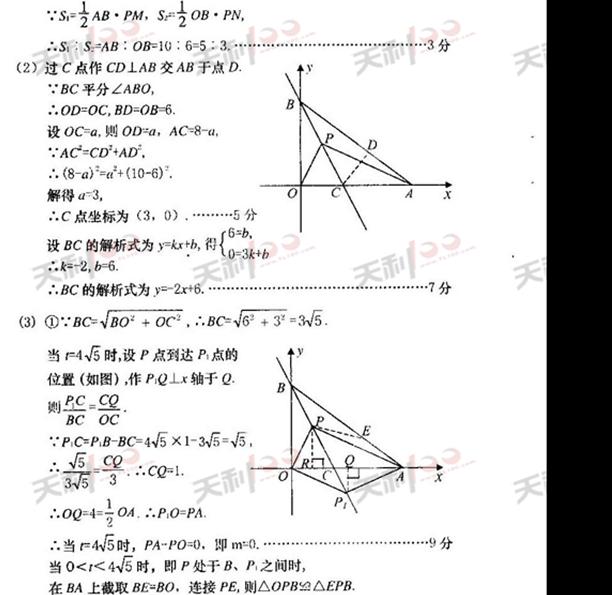
 (1)求抛物线的解析式;
(1)求抛物线的解析式;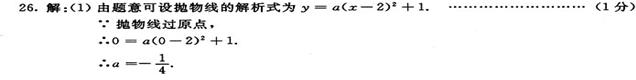
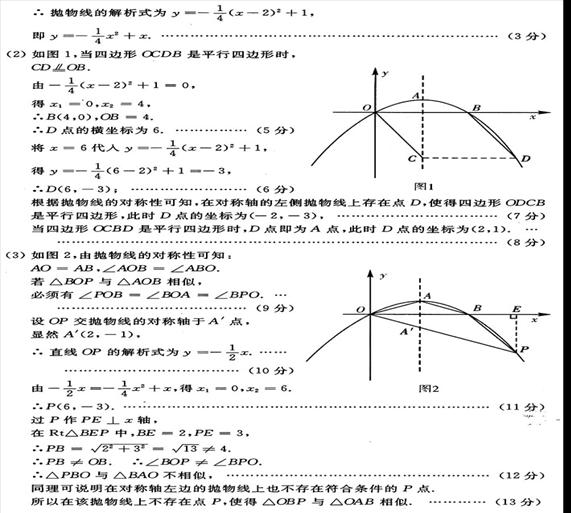
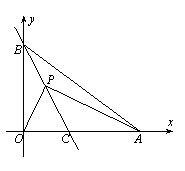 (2)求直线BC的解析式;
(2)求直线BC的解析式; 时,试求出m的取值范围;
时,试求出m的取值范围;

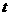 秒
秒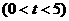 ,过P点作ED的平行线交AD于点M,过点M作AE的平行线交DE于点N.求四边形PMNE的面积S与时间
,过P点作ED的平行线交AD于点M,过点M作AE的平行线交DE于点N.求四边形PMNE的面积S与时间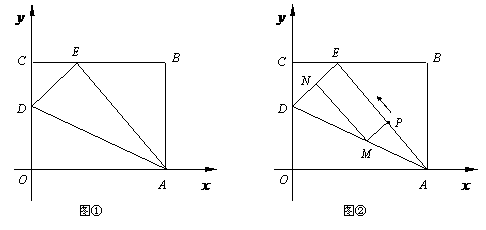
 中,
中,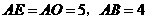
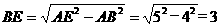 ∴
∴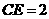
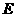 点坐标为
点坐标为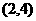 ………………………………………………………(2分)
………………………………………………………(2分) 中,
中,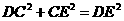 又∵
又∵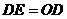
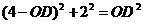 解得:
解得: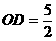
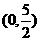 ………………………………………………………(3分)
………………………………………………………(3分)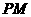 ∥
∥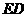 ∴
∴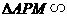
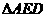
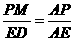 又知
又知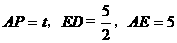
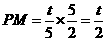 又∵
又∵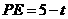
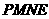 为矩形
为矩形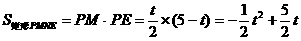 …………………(5分)∴
…………………(5分)∴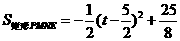 又∵
又∵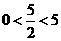
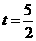 时,
时, 有最大值
有最大值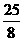 (面积单位)…………………(6分)
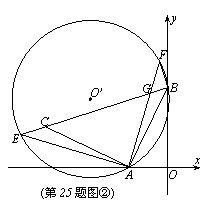
(面积单位)…………………(6分)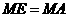 (如图①)
(如图①) 中,
中,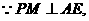 ∴
∴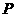 为
为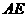 的中点
的中点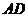 的中点
的中点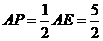 ∴
∴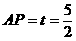 ∴
∴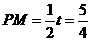
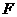 是关于
是关于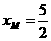 ,
,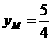
 为等腰三角形
为等腰三角形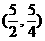 ………………………………………………(9分)
………………………………………………(9分)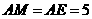 (如图②)
(如图②) 中,
中,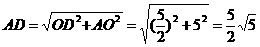
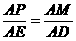
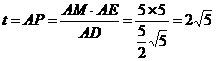 ∴
∴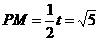
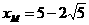 ,
, 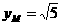
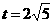 时(
时(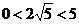 ),此时
),此时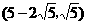
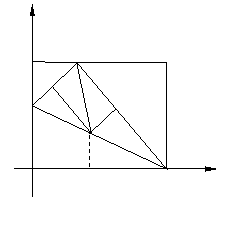
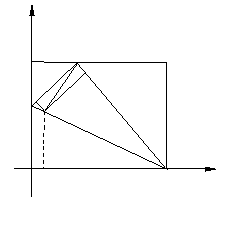 综合(i)、(ii)可知:
综合(i)、(ii)可知: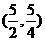 或
或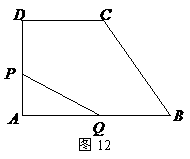 (广东梅州)如图12,直角梯形
(广东梅州)如图12,直角梯形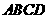 中,
中,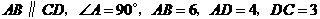 ,动点
,动点 出发,沿
出发,沿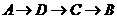 方向移动,动点
方向移动,动点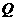 从点
从点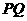 平分梯形
平分梯形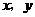 的取值范围;
的取值范围;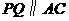 时,求
时,求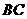 边上时,线段
边上时,线段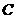 作
作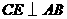 于
于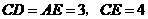 ,可得
,可得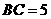 ,
,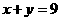 ,····························································· 2分
,····························································· 2分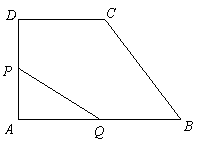 因为
因为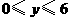 ,所以
,所以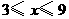 ,
,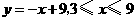 .·············· 3分
.·············· 3分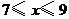 .
.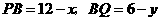 ,
,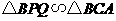 ,所以
,所以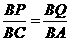 ,得··························· 4分
,得··························· 4分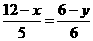 ,即
,即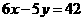 ,
,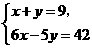 得
得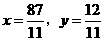 .··················································· 6分
.··················································· 6分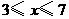 ,
,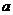 )当
)当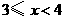 时,
时,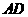 边上,
边上,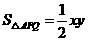 .
.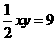 ········································· 8分
········································· 8分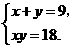 解得
解得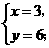 (
(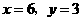 舍去).·········································· 9分
舍去).·········································· 9分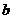 )当
)当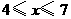 时,点
时,点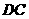 边上,此时
边上,此时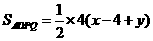 .
.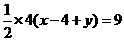 ,
,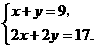 此方程组无解.
此方程组无解.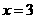 时,线段
时,线段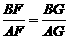 ,其中有且只有一个成立,请你判断哪一个结论成立,并证明成立的结论。
,其中有且只有一个成立,请你判断哪一个结论成立,并证明成立的结论。