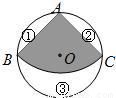
摘要:如图14.从一个直径是2的圆形铁皮中剪下一个圆心角为的扇形. (1)求这个扇形的面积(结果保留). (2)在剩下的三块余料中.能否从第③块余料中剪出一个圆作为底面与此扇形围成一个圆锥?请说明理由. (3)当的半径为任意值时.(2)中的结论是否仍然成立?请说明理由. 解:(1)连接.由勾股定理求得: ·································································· 1分 ································································· 2分 (2)连接并延长.与弧和交于. ····························································································· 1分 弧的长:······················································································ 2分 圆锥的底面直径为:··················································································· 3分 .不能在余料③中剪出一个圆作为底面与此扇形围成圆锥.·············· 4分 (3)由勾股定理求得: 弧的长:···················································································· 1分 圆锥的底面直径为:················································································ 2分 且 ···································································································· 3分 即无论半径为何值.··················································································· 4分 不能在余料③中剪出一个圆作为底面与此扇形围成圆锥.
网址:http://m.1010jiajiao.com/timu3_id_459824[举报]
 如图,从一个直径是2的圆形铁皮中剪下一个圆心角为90°的扇形
如图,从一个直径是2的圆形铁皮中剪下一个圆心角为90°的扇形(1)求这个扇形的面积(结果保留π)
(2)在剩下的三块余料中,能否从第③块余料中剪出一个圆作为底面与此扇形围成一个圆锥?请说明理由
(3)当⊙O的半径R(R>0)为任意值时,(2)中的结论是否仍然成立?请说明理由. 查看习题详情和答案>>
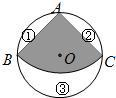
(2007•贵阳)如图,从一个直径是2的圆形铁皮中剪下一个圆心角为90°的扇形
(1)求这个扇形的面积(结果保留π)
(2)在剩下的三块余料中,能否从第③块余料中剪出一个圆作为底面与此扇形围成一个圆锥?请说明理由
(3)当⊙O的半径R(R>0)为任意值时,(2)中的结论是否仍然成立?请说明理由.
 查看习题详情和答案>>
查看习题详情和答案>>
(1)求这个扇形的面积(结果保留π)
(2)在剩下的三块余料中,能否从第③块余料中剪出一个圆作为底面与此扇形围成一个圆锥?请说明理由
(3)当⊙O的半径R(R>0)为任意值时,(2)中的结论是否仍然成立?请说明理由.
 查看习题详情和答案>>
查看习题详情和答案>>
 如图,从一个直径是1m的圆形铁皮中剪出一个圆心角为90°的扇形.
如图,从一个直径是1m的圆形铁皮中剪出一个圆心角为90°的扇形.