0 45883 45891 45897 45901 45907 45909 45913 45919 45921 45927 45933 45937 45939 45943 45949 45951 45957 45961 45963 45967 45969 45973 45975 45977 45978 45979 45981 45982 45983 45985 45987 45991 45993 45997 45999 46003 46009 46011 46017 46021 46023 46027 46033 46039 46041 46047 46051 46053 46059 46063 46069 46077 447348
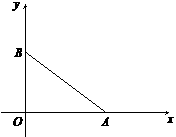
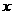 轴,建立如图所示的平面直角坐标系,点B在第一象限内。将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处。
轴,建立如图所示的平面直角坐标系,点B在第一象限内。将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处。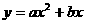 (
(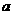 ≠0)经过C、A两点,求此抛物线的解析式;
≠0)经过C、A两点,求此抛物线的解析式;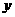 轴的平行线,交抛物线于点M。问:是否存在这样的点P,使得四边形CDPM为等腰梯形?若存在,请求出此时点P的坐标;若不存在,请说明理由。
轴的平行线,交抛物线于点M。问:是否存在这样的点P,使得四边形CDPM为等腰梯形?若存在,请求出此时点P的坐标;若不存在,请说明理由。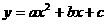 (
(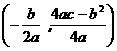 ,对称轴公式为
,对称轴公式为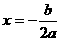

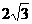
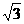 ,CH=3
,CH=3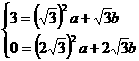 解得:
解得: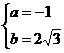
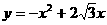
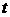 ,因为∠BOA=300,所以ON=
,因为∠BOA=300,所以ON=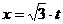 代入
代入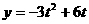
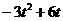 ),E(
),E(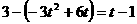 ,解得:
,解得: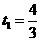 ,
,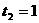 (舍)
(舍)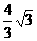 ,
,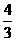 )
)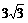 ).将
).将 绕AC的中点旋转1800,点O
绕AC的中点旋转1800,点O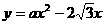 经过点A,点D是
经过点A,点D是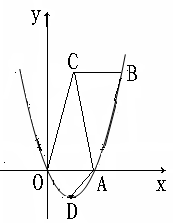 该抛物线的顶点.
该抛物线的顶点.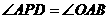 ,
,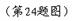
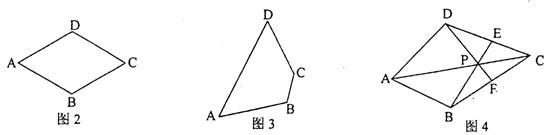

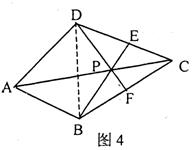 (2)如图3,点P即为所作点.……………………3分(答案不唯一.作图正确,无文字说明不扣分;无痕迹或痕迹不清晰的酌情扣分)
(2)如图3,点P即为所作点.……………………3分(答案不唯一.作图正确,无文字说明不扣分;无痕迹或痕迹不清晰的酌情扣分)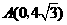 ,点
,点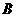 在
在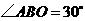 .动点
.动点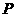 在线段
在线段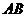 上从点
上从点 向点
向点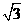 个单位的速度运动,设运动时间为
个单位的速度运动,设运动时间为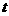 秒.在
秒.在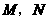 作等边
作等边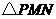 .
.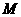 运动到与原点
运动到与原点 重合时
重合时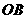 的中点
的中点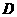 ,以
,以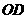 为边在
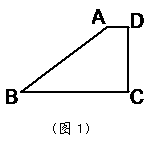
为边在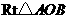 内部作如图2所示的矩形
内部作如图2所示的矩形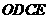 ,点
,点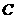 在线段
在线段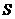 ,请求出当
,请求出当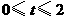 秒时
秒时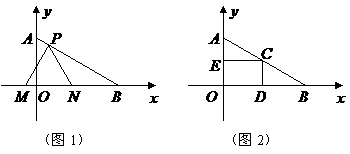
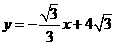 .
. ,
, ,
,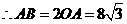 ,
,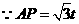 ,
,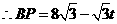 ,
,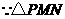 是等边三角形,
是等边三角形,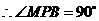 ,
,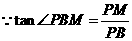 ,
,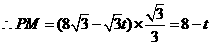 .
.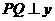 轴于
轴于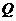 ,
,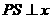 轴于
轴于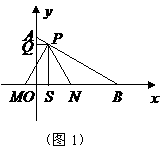 可求得
可求得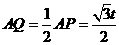 ,
,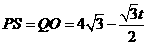 ,
,
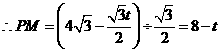 ,
, ,
,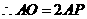 .
.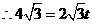 ,
,
 .
. 时,见图2.
时,见图2. 交
交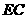 于点
于点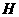 ,
, ,
,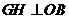 于
于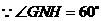 ,
,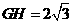 ,
,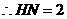 ,
,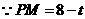 ,
,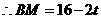 ,
,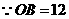 ,
,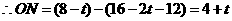 ,
,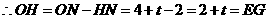 ,
,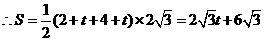 .
.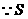 随
随 当
当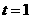 时,
时,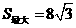 .
.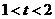 时,见图3.
时,见图3.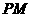 交
交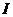 ,
,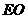 于点
于点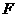 ,
,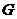 ,
,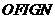 .
.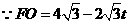 ,
,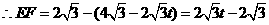 ,
,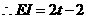 ,
,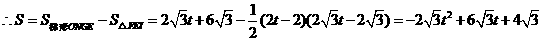 .
.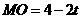 ,
,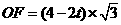 ,
,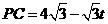 ,
,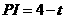 ,
,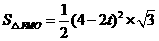
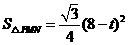 ,
,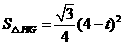
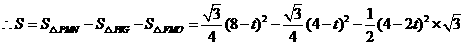
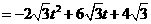 .
.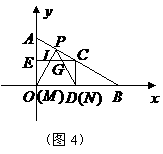
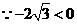 ,
,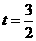 时,
时,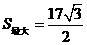 .
.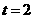 时,
时,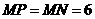 ,即
,即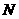 与
与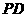 交
交 ,见图4.
,见图4.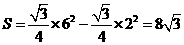 ,
,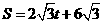 ;
;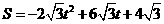 ;
;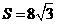 .
.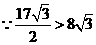 ,
,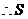 的最大值是
的最大值是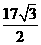 .
.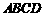 中,
中,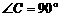 ,高
,高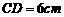 (如图1)。动点
(如图1)。动点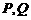 同时从点
同时从点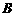 出发,点
出发,点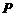 沿
沿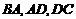 运动到点
运动到点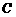 停止,点
停止,点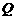 沿
沿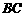 运动到点
运动到点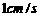 。而当点
。而当点 时,点
时,点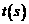 时,
时,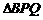 的面积为
的面积为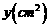 (如图2)。分别以
(如图2)。分别以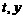 为横、纵坐标建立直角坐标系,已知点
为横、纵坐标建立直角坐标系,已知点 边上从
边上从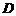 运动时,
运动时,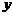 与
与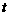 的函数图象是图3中的线段
的函数图象是图3中的线段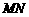 。
。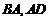 的长度;
的长度;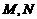 两点的坐标;
两点的坐标;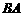 边上和
边上和 边上运动时,
边上运动时,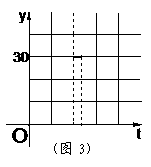

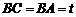 ,则
,则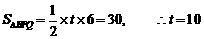 (秒)
(秒)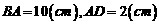 ;
;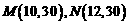
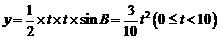 ;
;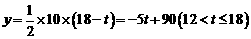
 (浙江温州)在
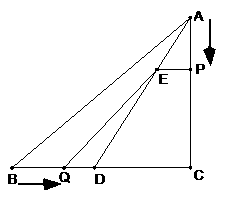
(浙江温州)在 中,
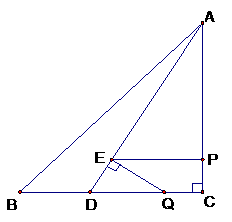
中,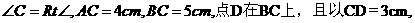 现有两个动点P、Q分别从点A和点B同时出发,其中点P以1cm/s的速度,沿AC向终点C移动;点Q以1.25cm/s的速度沿BC向终点C移动。过点P作PE∥BC交AD于点E,连结EQ。设动点运动时间为x秒。
现有两个动点P、Q分别从点A和点B同时出发,其中点P以1cm/s的速度,沿AC向终点C移动;点Q以1.25cm/s的速度沿BC向终点C移动。过点P作PE∥BC交AD于点E,连结EQ。设动点运动时间为x秒。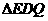 的面积为
的面积为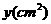 ,求
,求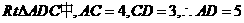 ,
,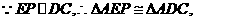
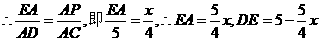
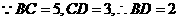 ,
,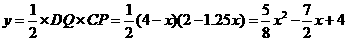
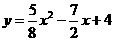 ,其中自变量的取值范围是:0<x<1.6
,其中自变量的取值范围是:0<x<1.6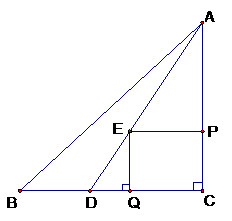 ①当
①当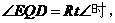
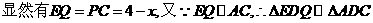
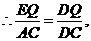
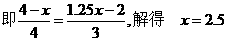
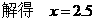
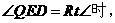
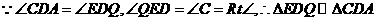
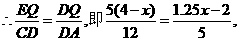
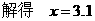
 的顶点
的顶点 的坐标(如图所示),写出图1,2,3中的顶点
的坐标(如图所示),写出图1,2,3中的顶点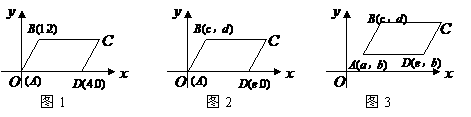
 的代数式表示);
的代数式表示);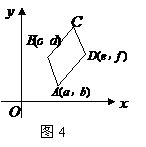
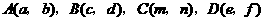 (如图4)时,则四个顶点的横坐标
(如图4)时,则四个顶点的横坐标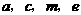 之间的等量关系为
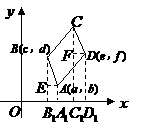
;纵坐标
之间的等量关系为
;纵坐标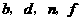 之间的等量关系为
(不必证明);
之间的等量关系为
(不必证明);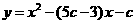 和三个点
和三个点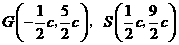 ,
,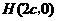 (其中
(其中 ).问当
).问当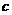 为何值时,该抛物线上存在点
为何值时,该抛物线上存在点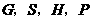 为顶点的四边形是平行四边形?并求出所有符合条件的
为顶点的四边形是平行四边形?并求出所有符合条件的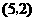 ,
,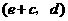 ,
,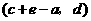 .···························································· 2分
.···························································· 2分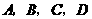 作
作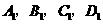 ,
, 分别过
分别过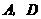 作
作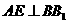 于
于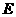 ,
,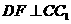 于点
于点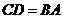 ,又
,又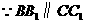 ,
,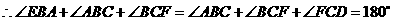 .
.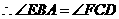 .
.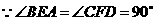 ,
,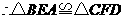 .·································································································· 5分
.·································································································· 5分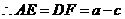 ,
,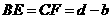 .
.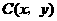 .由
.由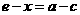 ,得
,得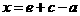 .
.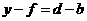 ,得
,得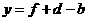 .
.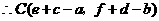 .································ 7分
.································ 7分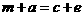 ,
,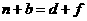 或
或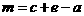 ,
,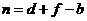 .························· 9分
.························· 9分 为平行四边形的对角线,由(3)可得
为平行四边形的对角线,由(3)可得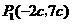 .要使
.要使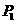 在抛物线上,
在抛物线上,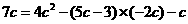 ,即
,即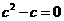 .
.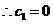 (舍去),
(舍去),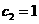 .此时
.此时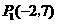 .································································ 10分
.································································ 10分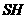 为平行四边形的对角线,由(3)可得
为平行四边形的对角线,由(3)可得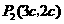 ,同理可得
,同理可得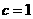 ,此时
,此时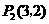 .
. 为平行四边形的对角线,由(3)可得
为平行四边形的对角线,由(3)可得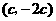 ,同理可得
,同理可得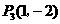 .
. (3)如果将直线AC作上下平移,交y轴于C’,交AB于A’,连结DC’,过点E作EF’∥DC’,交A’C’于F’,那么能否使四边形C’DEF’为正方形?若能,请求出正方形的面积;若不能,请说明理由。
(3)如果将直线AC作上下平移,交y轴于C’,交AB于A’,连结DC’,过点E作EF’∥DC’,交A’C’于F’,那么能否使四边形C’DEF’为正方形?若能,请求出正方形的面积;若不能,请说明理由。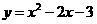 与x轴交A、B两点(A
与x轴交A、B两点(A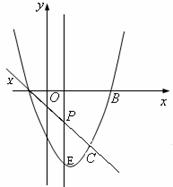 点在B点左侧),直线
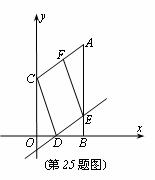
点在B点左侧),直线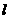 与抛物线交于A、C两点,其中
与抛物线交于A、C两点,其中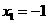 或
或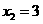 (1分)
(1分)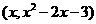 (1分)
(1分)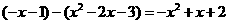 (2分)
(2分)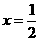 时,PE的最大值=
时,PE的最大值=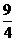 (1分)
(1分)