摘要:(五)证明题 27.已知:如图.AB∥CD.∠B=∠C.求证:∠E=∠F. [提示]证明AC∥BD. [答案]证明:∵ AB∥CD. ∴ ∠B=∠CDF(两直线平行.同位角相等). ∵ ∠B=∠C. ∴ ∠CDF=∠C. ∴ AC∥BD(内错角相等.两直线平行). ∴ ∠E=∠F(两直线平行.内错角相等). 28.已知:如图.AC∥DE.DC∥EF.CD平分∠BCD. 求证:EF平分∠BED. [提示]由AC∥DE.DC∥EF证∠1=∠3.由DC∥EF证∠2=∠4.再由CD平分∠BCA.即可证得∠3=∠4. [答案]证明:∵ AC∥DE. ∴ ∠1=∠5(两直线平行.内错角相等). 同理∠5=∠3. ∴ ∠1=∠3. ∵ DC∥EF. ∴ ∠2=∠4(两直线平行.同位角相等). ∵ CD平分∠ACB. ∴ ∠1=∠2. ∴ ∠3=∠4. ∴ EF平分∠BED. 29.已知:如图.AB∥CD.∠1=∠B.∠2=∠D.求证:BE⊥DE. [提示]过点E作EF∥AB.证明∠BED=90°. [答案]证明:过点E作EF∥AB. ∴ ∠BEF=∠B(两直线平行.内错角相等). ∵ ∠B=∠1. ∴ ∠BEF=∠1. 同理可证:∠DEF=∠2. ∵ ∠1+∠BEF+∠DEF+∠2=180°. 即2∠BEF+2∠DEF=180°. ∴ ∠BEF+∠DEF=90°. 即∠BED=90°. ∴ BE⊥DE. 30.已知:如图.AB∥CD.请你观察∠E.∠B.∠D之间有什么关系.并证明你所得的结论. [提示]结论:∠B+∠E=∠D.过点E作EF∥AB. [答案]结论:∠B+∠E=∠D. 证明:过点E作EF∥AB. ∴ ∠FEB=∠B(两直线平行.内错角相等). ∵ AB∥CD.EF∥AB. ∴ EF∥CD. ∴ ∠FED=∠D(两直线平行.内错角相等). ∵ ∠FED=∠FEB+∠BED=∠B+∠BED. ∴ ∠B+∠BED=∠D. 本题还可添加如图所示的辅助线.请你证明∠B+∠E=∠D. [点评]这是一道探索结论型的问题.要通过对直观图形仔细观察.大胆猜想.设定结论.再进行推理.验证结论.直观图形是观察思考的依据.准确的直观图形可引发正确的直觉思维.所以作图不可忽视.直觉思维是正确.还必须用相关的理论来验证.这样得到的结论方可靠.
网址:http://m.1010jiajiao.com/timu3_id_457606[举报]
填写证明的理由.
已知:如图,AB∥CD,EF、CG分别是∠AEC、∠ECD的角平分线;求证:EF∥CG.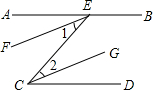
证明:∵AB∥CD(已知)
∴∠AEC=∠DCE ( )
又∵EF平分∠AEC (已知)
∴∠1=
∠AEC ( )
同理∠2=
∠DCE,∴∠1=∠2
∴EF∥CG ( )
查看习题详情和答案>>
已知:如图,AB∥CD,EF、CG分别是∠AEC、∠ECD的角平分线;求证:EF∥CG.

证明:∵AB∥CD(已知)
∴∠AEC=∠DCE (
又∵EF平分∠AEC (已知)
∴∠1=
| 1 |
| 2 |
同理∠2=
| 1 |
| 2 |
∴EF∥CG (
 16、如图,AC是菱形ABCD的对角线,请你在下列条件:①分别作∠BAC、∠DAC的平分线AE、AF交BC于点E,交DC于点F;②作AE⊥BC于点E,AF⊥DC于点F.从中任选一个作为条件,证明BE=DF.
16、如图,AC是菱形ABCD的对角线,请你在下列条件:①分别作∠BAC、∠DAC的平分线AE、AF交BC于点E,交DC于点F;②作AE⊥BC于点E,AF⊥DC于点F.从中任选一个作为条件,证明BE=DF.已知:如图,AC是菱形ABCD的对角线,
①
(填写选择条件的序号).求证:BE=DF.
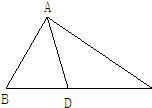 30、附加题2:已知:如图,△ABC中,AD平分∠BAC,∠B=65°,∠C=35度.求∠BAD的度数.
30、附加题2:已知:如图,△ABC中,AD平分∠BAC,∠B=65°,∠C=35度.求∠BAD的度数.
 ,其它条件不变,你能猜出MN的长度吗?请用简洁的语言表达你发现的规律.
,其它条件不变,你能猜出MN的长度吗?请用简洁的语言表达你发现的规律.