摘要:27.已知抛物线:(.为常数.且.)的顶点为.与轴交于点,抛物线与抛物线关于轴对称.其顶点为.连接... 注:抛物线的顶点坐标为. (1)请在横线上直接写出抛物线的解析式: , (2)当时.判定的形状.并说明理由, (3)抛物线上是否存在点.使得四边形为菱形?如果存在.请求出的值,如果不存在.请说明理由. 解:(1). (2)当时.为等腰直角三角形. 理由如下: 如图:点与点关于轴对称.点又在轴上. . 过点作抛物线的对称轴交轴于.过点作于. 当时.顶点的坐标为.. 又点的坐标为. .. 从而.. 由对称性知.. 为等腰直角三角形. (3)假设抛物线上存在点.使得四边形为菱形.则. 由(2)知... 从而为等边三角形. . 四边形为菱形.且点在上.点与点关于对称. 与的交点也为点.因此. 点的坐标分别为. . 在中.. .. 故抛物线上存在点.使得四边形为菱形.此时.
网址:http://m.1010jiajiao.com/timu3_id_454617[举报]
已知抛物线![]() :
:![]() (
(![]() 为常数,且
为常数,且![]() )的顶点为
)的顶点为![]() ,与
,与![]() 轴交于点
轴交于点![]() ;抛物线
;抛物线![]() 与抛物线
与抛物线![]() 关于
关于![]() 轴对称,其顶点为
轴对称,其顶点为![]() .若点
.若点![]() 是抛物线
是抛物线![]() 上的点,使得以A、B、C、P为顶点的四边形为菱形,则m为( )
上的点,使得以A、B、C、P为顶点的四边形为菱形,则m为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看习题详情和答案>>
已知抛物线 :
: (
( 为常数,且
为常数,且 )的顶点为
)的顶点为 ,与
,与 轴交于点
轴交于点 ;抛物线
;抛物线 与抛物线
与抛物线 关于
关于 轴对称,其顶点为
轴对称,其顶点为 。若点
。若点 是抛物线
是抛物线 上的点,使得以A、B、C、P为顶点的四边形为菱形,则m为(
)
上的点,使得以A、B、C、P为顶点的四边形为菱形,则m为(
)
(A)、 (B)、
(B)、 (C)、
(C)、 (D)、
(D)、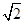
查看习题详情和答案>>
已知抛物线 :
: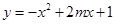 (
( 为常数,且
为常数,且 )的顶点为
)的顶点为 ,与
,与 轴交于点
轴交于点 ;抛物线
;抛物线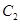 与抛物线
与抛物线 关于
关于 轴对称,其顶点为
轴对称,其顶点为 .若点
.若点 是抛物线
是抛物线 上的点,使得以A、B、C、P为顶点的四边形为菱形,则m为( )
上的点,使得以A、B、C、P为顶点的四边形为菱形,则m为( )

A. B.
B. C.
C. D.
D.
查看习题详情和答案>>
 :
: (
( 为常数,且
为常数,且 )的顶点为
)的顶点为 ,与
,与 轴交于点
轴交于点 ;抛物线
;抛物线 与抛物线
与抛物线 。若点
。若点 是抛物线
是抛物线 B.
B. C.
C. D.
D.