摘要:25. 已知:如图.A(0,1)是y轴上一定点.B是x轴上一动点.以AB为边.在∠OAB的外部作∠BAE=∠OAB .过B作BC⊥AB.交AE于点C. (1)当B点的横坐标为时.求线段AC的长, (2)当点B在x轴上运动时.设点C的纵.横坐标分别为y.x.试求y与x的函数关系式(当点B运动到O点时.点C也与O点重合), 的直线l与(2)中所求函数的图象有两个公共点M1(x1.y1).M2(x2.y2).且x12+x22-6(x1+x2)=8.求直线l的解析式. 解:(1)方法一:在Rt△AOB中.可求得AB= ∵∠OAB=∠BAC.∠AOB=∠ABC=Rt∠ .∴△ABO∽△ABC .∴.由此可求得:AC= 方法二:由题意知:tan∠OAB= (2)方法一:当B不与O重合时.延长CB交y轴于点D.过C作CH⊥x轴.交x轴于点H.则可证得AC=AD.BD=--4′ ∵AO⊥OB.AB⊥BD.∴△ABO∽△BDO.则OB2=AO×OD----6′.即 化简得:y=.当O.B.C三点重合时.y=x=0.∴y与x的函数关系式为:y= 方法二:过点C作CG⊥x轴.交AB的延长线于点H.则AC2=(1-y)2+x2=(1+y)2.化简即可得. (3)设直线的解析式为y=kx+b.则由题意可得:.消去y得:x2-4kx-4b=0.则有.由题设知: x12+x22-6(x1+x2)=8.即(4k)2+8b-24k=8.且b=-1.则16k2-24k -16=0.解之得:k1=2.k2=.当k1=2.b=-1时. △=16k2+16b=64-16>0.符合题意,当k2=.b=-1时.△=16k2+16b=4-16<0.不合题意.∴所求的直线l的解析式为:y=2x-1
网址:http://m.1010jiajiao.com/timu3_id_454615[举报]
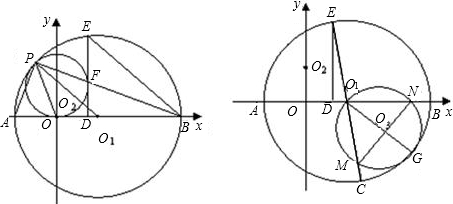
已知:如图,直线 y=-
x+3交x轴于O1,交y轴于O2,⊙O2与x轴相切于O点,交直线O1O2于P点,以O1为圆心O1P为半径的圆交x轴于A、B两点,PB交⊙O2于点F,⊙O1的弦BE=BO,EF的延长线交AB于D,连接PA、PO.
(1)求证:∠APO=∠BPO;
(2)求证:EF是⊙O2的切线;
(3)EO1的延长线交⊙O1于C点,若G为BC上一动点,以O1G为直径作⊙O3交O1C于点M,交O1B于N.下列结论:①O1M•O1N为定值;②线段MN的长度不变.只有一个是正确的,请你判断出正确的结论,并证明正确的结论,以及求出它的值.
 查看习题详情和答案>>
查看习题详情和答案>>
| 3 | 4 |
(1)求证:∠APO=∠BPO;
(2)求证:EF是⊙O2的切线;
(3)EO1的延长线交⊙O1于C点,若G为BC上一动点,以O1G为直径作⊙O3交O1C于点M,交O1B于N.下列结论:①O1M•O1N为定值;②线段MN的长度不变.只有一个是正确的,请你判断出正确的结论,并证明正确的结论,以及求出它的值.
 查看习题详情和答案>>
查看习题详情和答案>>
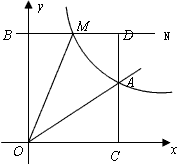
 已知:如图,正比例函数y=ax的图象与反比例函数y=
已知:如图,正比例函数y=ax的图象与反比例函数y= 的图象交于点A(3,2)
的图象交于点A(3,2)
(1)试确定上述正比例函数和反比例函数的表达式;
(2)根据图象回答,在第一象限内,当x取何值时,反比例函数的值大于正比例函数的值?
(3)点M(m,n)是反比例函数图象上的一动点,其中0<m<3,过点M作直线MB∥x轴,交y轴于点B;过点A作直线AC∥y轴交x轴于点C,交直线MB于点D.当四边形OADM的面积为6时,请判断线段BM与DM的大小关系,并说明理由.
查看习题详情和答案>>
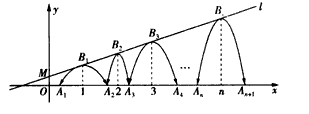
已知:如图,直线l: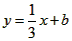 经过点
经过点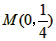 ,一组抛物线的顶点B1(1,y1),B2(2,y2),B3(3,y3),…,Bn(n,yn)(n为正整数)依次是直线l上的点,这组抛物线与x轴正半轴的交点依次是:A1(x1,0),A2(x2,0),A3(x3,0),…,An+1(xn+1,0)(n为正整数),设x1=d(0<d<1)。
,一组抛物线的顶点B1(1,y1),B2(2,y2),B3(3,y3),…,Bn(n,yn)(n为正整数)依次是直线l上的点,这组抛物线与x轴正半轴的交点依次是:A1(x1,0),A2(x2,0),A3(x3,0),…,An+1(xn+1,0)(n为正整数),设x1=d(0<d<1)。
(1)求b的值;
(2)求经过点A1、B1、A2的抛物线的解析式(用含d的代数式表示);
(3)定义:若抛物线的顶点与x轴的两个交点构成的三角形,则这种抛物线就称为“美丽抛物线”。
探究:当d(0<d<1)的大小变化时,这组抛物线中是否存在美丽抛物线?若存在,清你求出相应的d 的值。
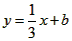 经过点
经过点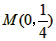 ,一组抛物线的顶点B1(1,y1),B2(2,y2),B3(3,y3),…,Bn(n,yn)(n为正整数)依次是直线l上的点,这组抛物线与x轴正半轴的交点依次是:A1(x1,0),A2(x2,0),A3(x3,0),…,An+1(xn+1,0)(n为正整数),设x1=d(0<d<1)。
,一组抛物线的顶点B1(1,y1),B2(2,y2),B3(3,y3),…,Bn(n,yn)(n为正整数)依次是直线l上的点,这组抛物线与x轴正半轴的交点依次是:A1(x1,0),A2(x2,0),A3(x3,0),…,An+1(xn+1,0)(n为正整数),设x1=d(0<d<1)。(1)求b的值;
(2)求经过点A1、B1、A2的抛物线的解析式(用含d的代数式表示);
(3)定义:若抛物线的顶点与x轴的两个交点构成的三角形,则这种抛物线就称为“美丽抛物线”。
探究:当d(0<d<1)的大小变化时,这组抛物线中是否存在美丽抛物线?若存在,清你求出相应的d 的值。
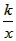 的图象交于点A(3,2)。
的图象交于点A(3,2)。