摘要:已知关于x的二次函数与.这两个二次函数的图象中的一条与x轴交于A, B两个不同的点. (l)试判断哪个二次函数的图象经过A, B两点, .试求B点坐标, 的条件下.对于经过A, B两点的二次函数.当x取何值时.y的值随x值的增大而减小? 解:(l)对于关于x的二次函数y = 由于△=(-m ) 2-4×l×=-m2-2<0, 所以此函数的图象与x轴没有交点 对于关于x的二次函数 y =. 由于△=(-m ) 2-4 ×l×=-m2-2<0, 所以此函数的图象与x轴没有交点 对于关于x的二次函数 由于 所以此函数的图象与x轴有两个不同的交点. 故图象经过A.B两点的二次函数为 代入.得=0. 整理.得m2-2m = 0 . 解之.得m=0.或m = 2. 当m =0时.y=x2-1.令y = 0.得x2-1 = 0. 解这个方程.得x1=-1.x2=1 此时.B点的坐标是B . 当m=2时.y=x2-2x-3.令y=0.得x2-2x-3=0. 解这个方程.得x1=-1.x2=3 此时.B点的坐标是B(3.0). (3) 当m =0时.二次函数为y=x2-1.此函数的图象开口向上.对称轴为x=0.所以当x<0时.函数值 y 随:的增大而减小. 当m=2时.二次函数为y = x2-2 x-3 = (x-1)2-4, 此函数的图象开口向上.对称轴为x = l.所以当x < l 时.函数值y随x的增大而减小.
网址:http://m.1010jiajiao.com/timu3_id_454620[举报]
已知关于![]() 的一元二次方程
的一元二次方程![]() 有实数根,
有实数根,![]() 为正整数.
为正整数.
(1)求![]() 的值;
的值;
(2)当此方程有两个非零的整数根时,将关于![]() 的二次函数
的二次函数![]() 的图象向下平移8个单位,求平移后的图象的解析式;
的图象向下平移8个单位,求平移后的图象的解析式;
(3)在(2)的条件下,将平移后的二次函数的图象在![]() 轴下方的部分沿
轴下方的部分沿![]() 轴翻折,图象的其余部分保持不变,得到一个新的图象.请你结合这个新的图象回答:当直线
轴翻折,图象的其余部分保持不变,得到一个新的图象.请你结合这个新的图象回答:当直线
![]() 与此图象有两个公共点时,
与此图象有两个公共点时,![]() 的取值范围.
的取值范围.
已知关于![]() 的方程
的方程![]() .
.
1.若方程有两个不相等的实数根,求![]() 的取值范围;
的取值范围;
2. 若正整数![]() 满足
满足![]() ,设二次函数
,设二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 两点,将此图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,得到一个新的图象.请你结合这个新的图象回答:当直线
两点,将此图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,得到一个新的图象.请你结合这个新的图象回答:当直线![]() 与此图象恰好有三个公共点时,求出
与此图象恰好有三个公共点时,求出![]() 的值(只需要求出两个满足题意的k值即可).
的值(只需要求出两个满足题意的k值即可).
查看习题详情和答案>>
已知关于 的一元二次方程
的一元二次方程 .
.
(1)求证:方程有两个实数根;
(2)当此方程有一个根是 时,求关于
时,求关于 的二次函数
的二次函数 的表达式;
的表达式;
(3)在(2)的条件下,若点A 与点B
与点B (
( )在关于
)在关于 的二次函数
的二次函数 的图象上,将此二次函数的图象在
的图象上,将此二次函数的图象在 上方的部分沿
上方的部分沿 翻折,图象的其它部分保持不变,得到一个新图象,当这个新图象与x轴恰好只有两个公共点时,n的取值范围是_________________________________________.
翻折,图象的其它部分保持不变,得到一个新图象,当这个新图象与x轴恰好只有两个公共点时,n的取值范围是_________________________________________.
 的一元二次方程
的一元二次方程 .
. 时,求关于
时,求关于 的表达式;
的表达式; 与点B
与点B (
( )在关于
)在关于 上方的部分沿
上方的部分沿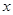 的方程
的方程 .
. 的取值范围;
的取值范围; ,设二次函数
,设二次函数 的图象与
的图象与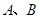 两点,将此图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,得到一个新的图象.请你结合这个新的图象回答:当直线
两点,将此图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,得到一个新的图象.请你结合这个新的图象回答:当直线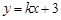 与此图象恰好有三个公共点时,求出
与此图象恰好有三个公共点时,求出 的值(只需要求出两个满足题意的k值即可).
的值(只需要求出两个满足题意的k值即可).