摘要：22．已知抛物线y＝ax2+bx+c经过点(1.2). (1)若a＝1.抛物线顶点为A.它与x轴交于两点B.C.且△ABC为等边三角形.求b的值. (2)若abc＝4.且a≥b≥c.求|a|+|b|+|c|的最小值. 解:⑴由题意.a+b+c＝2. ∵a＝1.∴b+c＝1 抛物线顶点为A 设B(x1.0).C(x2.0).∵x1+x2＝-b.x1x2＝c.△＝b2-4c＞0 ∴|BC|＝| x1-x2|＝＝＝ ∵△ABC为等边三角形.∴ -c＝ 即b2-4c＝2·.∵b2-4c＞0.∴＝2 ∵c＝1-b. ∴b2+4b-16＝0. b＝-2±2 所求b值为-2±2 ⑵∵a≥b≥c.若a＜0.则b＜0.c＜0.a+b+c＜0.与a+b+c＝2矛盾. ∴a＞0． ∵b+c＝2-a.bc＝ ∴b.c是一元二次方程x2-(2-a)x+＝0的两实根． ∴△＝(2-a)2-4×≥0. ∴a3-4a2+4a-16≥0, 即(a2+4)(a-4)≥0.故a≥4. ∵abc＞0.∴a.b.c为全大于0或一正二负． ①若a.b.c均大于0.∵a≥4.与a+b+c＝2矛盾, ②若a.b.c为一正二负.则a＞0.b＜0.c＜0, 则|a|+|b|+|c|＝a-b-c＝a-(2-a)＝2a-2. ∵ a≥4.故2a-2≥6 当a＝4.b＝c＝-1时.满足题设条件且使不等式等号成立． 故|a|+|b|+|c|的最小值为6．
网址：http://m.1010jiajiao.com/timu3_id_454612[举报]
已知抛物线y＝ax2＋bx＋c经过点A(－1，0)，且经过直线y＝x－3与x轴的交点B及与y轴的交点C．
(1)求抛物线的解析式；
(2)求抛物线的顶点坐标；
(3)若点M在第四象限内的抛物线上，且OM⊥BC，垂足为D，求点M的坐标．
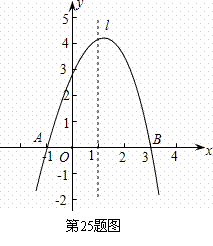
查看习题详情和答案>>已知抛物线y＝ax2＋bx＋c经过A(－1，0)、B(3，0)、C(0，3)三点，直线l是抛物线的对称轴．
(1)求抛物线的函数关系式；
(2)设点P是直线l上的一个动点，当△PAC的周长最小时，求点P的坐标；
(3)在直线l上是否存在点M，使△MAC为等腰三角形？若存在，直接写出所有符合条件的点M的坐标；若不存在，请说明理由．
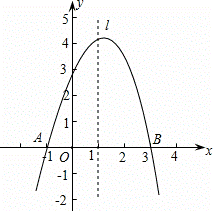
已知抛物线y＝ax2＋bx＋c经过A(－1，0)、B(3，0)、C(0，3)三点，直线l是抛物线的对称轴．
(1)求抛物线的函数关系式；
(2)设点P是直线l上的一个动点，当△PAC的周长最小时，求点P的坐标；
(3)在直线l上是否存在点M，使△MAC为等腰三角形？若存在，直接写出所有符合条件的点M的坐标；若不存在，请说明理由．
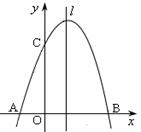(1)求抛物线的解析式和对称轴； 
时，求直线AN的解析式.