摘要:(四)图形与证明 ⒈了解证明的含义 考试内容: 定义.命题.逆命题.定理.定理的证明.反证法. 考试要求: (1)理解证明的必要性. (2)通过具体的例子.了解定义.命题.定理的含义.会区分命题的条件和结论. (3)结合具体例子.了解逆命题的概念.会识别两个互逆命题.并知道原命题成立其逆命题不一定成立. (4)理解反例的作用.知道利用反例可以证明一个命题是错误的. (5)通过实例.体会反证法的含义. (6)掌握用综合法证明的格式.体会证明的过程要步步有据. ⒉掌握证明的依据 考试内容: 一条直线截两条平行直线所得的同位角相等, 两条直线被第三条直线所截.若同位角相等.那么这两条直线平行, 若两个三角形的两边及其夹角分别相等.则这两个三角形全等, 两个三角形的两角及其夹边分别相等.则这两个三角形全等, 两个三角形的三边分别相等.则这两个三角形全等, 全等三角形的对应边.对应角分别相等. 考试要求: 运用以上6条“基本事实 作为证明命题的依据. ⒊利用2中的基本事实证明下列命题 考试内容: (1)平行线的性质定理(内错角相等.同旁内角互补)和判定定理(内错角相等或同旁内角互补.则两直线平行). (2)三角形的内角和定理及推论(三角形的外角等于不相邻的两内角的和.三角形的外角大于任何一个和它不相邻的内角). (3)直角三角形全等的判定定理. (4)角平分线性质定理及逆定理,三角形的三条角平分线交于一点. (5)垂直平分线性质定理及逆定理,三角形的三边的垂直平分线交干一点. (6)三角形中位线定理. (7)等腰三角形.等边三角形.直角三角形的性质和判定定理. (8)平行四边形.矩形.菱形.正方形.等腰梯形的性质和判定定理. 考试要求: (1)会利用2中的基本事实证明上述命题. (2)会利用上述定理证明新的命题. (3)练习和考试中与证明有关的题目难度.应与上述所列的命题的论证难度相当. ⒋通过对欧几里得的介绍.感受几何的演绎体系对数学发展和人类文明的价值. 统 计 与 概 率 ⒈统计 考试内容: 数据.数据的收集.整理.描述和分析. 抽样.总体.个体.样本. 扇形统计图. 加权平均数.数据的集中程度与离散程度.极差和方差. 频数.频率.频数分布.频数分布表.直方图.折线图. 样本估计总体.样本的平均数.方差.总体的平均数.方差. 统计与决策.数据信息.统计在社会生活及科学领域中的应用. 考试要求: (1)会收集.整理.描述和分析数据.能用计算器处理较为复杂的统计数据. (2)了解抽样的必要性.能指出总体.个体.样本.知道不同的抽样可能得到不同的结果. (3)会用扇形统计图表示数据. (4)理解并会计算加权平均数.能根据具体问题.选择合适的统计量表示数据的集中程度. (5)会探索如何表示一组数据的离散程度.会计算极差与方差.并会用它们表示数据的离散程度. (6)理解频数.频率的概念.了解频数分布的意义和作用.会列频数分布表.画频数分布直方图和频数折线图.并能解决简单的实际问题. (7)体会用样本估计总体的思想.能用样本的平均数.方差来估计总体的平均数和方差. (8)能根据统计结果做出合理的判断和预测.体会统计对决策的作用.能比较清晰地表达自己的观点.并进行交流. (9)能根据问题查找相关资料.获得数据信息.会对日常生活中的某些数据发表自己的看法. (10)能应用统计知识解决在社会生活及科学领域中一些简单的实际问题. ⒉概率 考试内容: 事件.事件的概率.列举法计算简单事件的概率. 实验与事件发生的频率.大量重复实验与事件发生概率的估计. 运用概率知识解决实际问题. 考试要求: (1)在具体情境中了解概率的意义.运用列举法计算简单事件发生的概率. (2)通过实验.获得事件发生的频率,知道大量重复实验时频率可作为事件发生概率的估计值. (3)会通过实验获得事件发生的概率.并能运用概率知识解决一些实际问题. 课 题 学 习 考试内容: 课题的提出.数学模型.问题解决. 数学知识的应用.研究问题的方法. 考试要求: (1)结合实际.会提出.探讨一些具有挑战性的研究课题.经历“问题情境-建立模型-求解-解释与应用 的基本过程.进而体验从实际问题抽象出数学问题.建立数学模型.综合应用已有的知识解决问题的过程.加深理解相关的数学知识.发展思维能力. (2)体验数学知识之间的内在联系.初步形成对数学整体性的认识. (3)理解数学知识在实际问题中的应用.初步掌握一些研究问题的方法与经验.
网址:http://m.1010jiajiao.com/timu3_id_453802[举报]
已知:如图,AB是⊙O的一条弦,点C为![]() 的中点,CD是⊙O的直径,过C点的直线
的中点,CD是⊙O的直径,过C点的直线![]() 交AB所在直线于点E,交⊙O于点F。
交AB所在直线于点E,交⊙O于点F。
(1
)判定图中(2
)将直线
 查看习题详情和答案>>
查看习题详情和答案>>
我们知道,两边及其中一边的对角分别对应相等的两个三角形不一定全等.那么在什么情况下,它们会全等
(1)阅读与证明:
对于这两个三角形均为直角三角形,显然它们全等.
对于这两个三角形均为钝角三角形,可证它们全等(证明略).
对于这两个三角形均为锐角三角形,它们也全等,可证明如下:
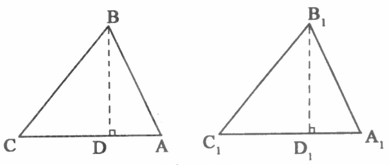
已知:△ABC、△A1B1C1均为锐角三角形,AB=A1B1,BC=B1Cl,∠C=∠Cl.
求证:△ABC≌△A1B1C1.
(请你将下列证明过程补充完整.)
证明:分别过点B,B1作BD⊥CA于D,B1 D1⊥C1 A1于D1.
则∠BDC=∠B1D1C1=900,
∵BC=B1C1,∠C=∠C1,
∴△BCD≌△B1C1D1,-
∴BD=B1D1.
(2)归纳与叙述:
由(1)可得到一个正确结论,请你写出这个结论.
下列命题:①正多边形都是轴对称图形;②通过对足球迷健康状况的调查可以了解我国公民的健康状况;③方程
-
=
的解是x=0;④如果一个角的两边与另一个角的两边分别平行,那么这两个角相等.其中真命题的个数有( )
| 1 |
| x2-1 |
| 2 |
| x+1 |
| 3 |
| x-1 |
| A、1个 | B、2个 | C、3个 | D、4个 |
