0 447096 447104 447110 447114 447120 447122 447126 447132 447134 447140 447146 447150 447152 447156 447162 447164 447170 447174 447176 447180 447182 447186 447188 447190 447191 447192 447194 447195 447196 447198 447200 447204 447206 447210 447212 447216 447222 447224 447230 447234 447236 447240 447246 447252 447254 447260 447264 447266 447272 447276 447282 447290 447348
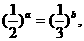 下列五个关系式
下列五个关系式 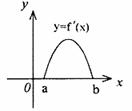 7 、
7 、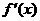 是
是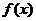 的导函数,
的导函数,
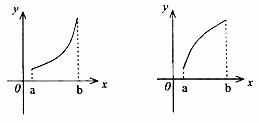
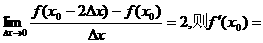 ( )
( )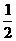 B.-1 C.0 D.-2
B.-1 C.0 D.-2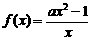 的单调递增区间为
的单调递增区间为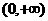 ,那么实数a的取值范围是 ( )
,那么实数a的取值范围是 ( )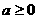 B.
B.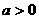 C.
C.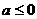 D.
D.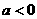
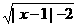 的定义域是(-∞,-1
的定义域是(-∞,-1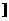 ∪[3,+∞
∪[3,+∞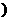 ,则( )
,则( )
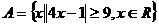 ,
, 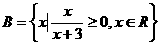 , 则A∩B=
, 则A∩B=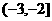 (B)
(B)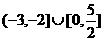 (C)
(C)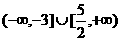 (D)
(D)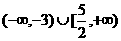
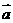 |=1,|
|=1,|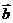 |=
|=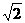 ,
,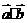 ; (II)若
; (II)若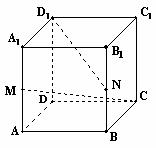 (I)CM与D1N所成角的余弦值;
(I)CM与D1N所成角的余弦值; (II)
若AN的长度不少于6米,则当AM、AN的长度是多少时,矩形AMPN的面积最 小?并求出最小面积.
(II)
若AN的长度不少于6米,则当AM、AN的长度是多少时,矩形AMPN的面积最 小?并求出最小面积. ,|BC|=2|AC|.
,|BC|=2|AC|.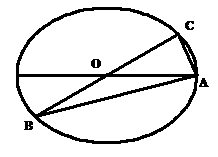 (II)如果椭圆上有两点P、Q,使∠PCQ的平分线垂直于AO,
(II)如果椭圆上有两点P、Q,使∠PCQ的平分线垂直于AO,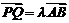 .
.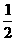 的等比数列,Sn是其前n项和.
的等比数列,Sn是其前n项和.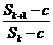 >3成立?证明你的论断.
>3成立?证明你的论断.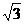 ,五个顶点都在同一个球面上,则此球的表面积为
.
,五个顶点都在同一个球面上,则此球的表面积为
.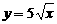 上与直线2x-y-4=0平行的切线的纵截距是 .
上与直线2x-y-4=0平行的切线的纵截距是 .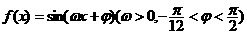 ,给出以下四个论断:
,给出以下四个论断: 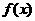 的周期为π; ②
的周期为π; ②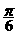 ,0)上是增函数;
,0)上是增函数; 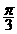 ,0)对称; ④
,0)对称; ④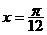 对称.
对称.  (只需将命题的序号填在横线上).
(只需将命题的序号填在横线上).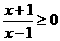 的解集是
的解集是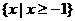 (B)
(B) 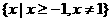
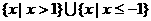 (D)
(D)
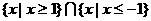
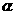 是第二象限的角,且
是第二象限的角,且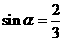 ,则
,则
 (B)
(B)
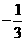 (C)
(C)
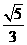 (D)
(D)
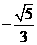
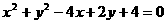 (B)
(B)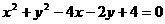
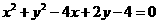 (D)
(D)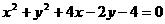
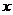 都成立的一个是
都成立的一个是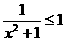 (B)
(B)
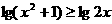 (C)
(C)
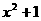
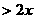 (D)
(D)
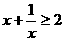
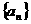 中,
中,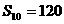 ,那么
,那么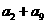 的值是
的值是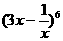 的展开式的常数项是
的展开式的常数项是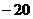 (C)540 (D)
(C)540 (D)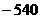
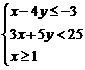 ,则
,则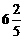 ,z无最大值
,z无最大值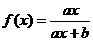 且不等式
且不等式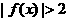 的解集为
的解集为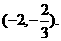
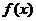 的解析式;
的解析式;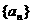 满足:
满足: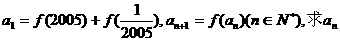 ;
;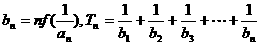 ,数列
,数列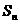 ,求证:
,求证: