0 446164 446172 446178 446182 446188 446190 446194 446200 446202 446208 446214 446218 446220 446224 446230 446232 446238 446242 446244 446248 446250 446254 446256 446258 446259 446260 446262 446263 446264 446266 446268 446272 446274 446278 446280 446284 446290 446292 446298 446302 446304 446308 446314 446320 446322 446328 446332 446334 446340 446344 446350 446358 447348
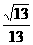 B
B 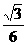 C
C 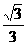 D
D 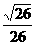
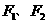 ,以
,以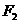 为圆心作圆经过椭圆中心,且与椭圆相交于M点,直线
为圆心作圆经过椭圆中心,且与椭圆相交于M点,直线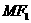 与圆相切,则该椭圆的离心率e=(
)
与圆相切,则该椭圆的离心率e=(
)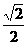 B
B 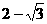 C
C
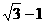 D
D 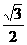
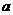 、b为不相等的两个正数,若A是
、b为不相等的两个正数,若A是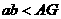 B
B 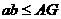 C
C 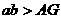 D
D
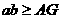
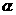 的终边经过点
的终边经过点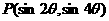 ,且
,且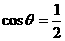 ,则
,则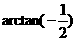 B
B  C
C  D
D 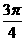
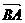 与x轴正方向的夹角为
与x轴正方向的夹角为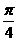 B
B
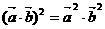
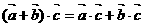 D 若
D 若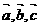 为非零向量,且
为非零向量,且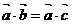 则
则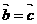
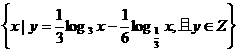 ,若
,若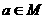 ,则
,则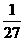 B
B 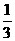 C 3
D 9
C 3
D 9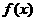 ,若存在
,若存在 成立,则称
成立,则称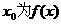 的不动点。如果函数
的不动点。如果函数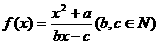 有且只有两个不动点0,2,且
有且只有两个不动点0,2,且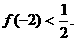
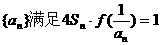 ,求数列通项
,求数列通项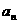 ;
;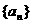 满足
满足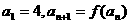 ,求证:当
,求证:当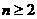 时,恒有
时,恒有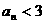 成立.
成立.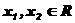 ,常数
,常数 ,定义运算“
,定义运算“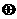 :
: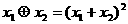 ”;“ :
”;“ :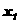
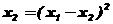 ”
” (I)若
(I)若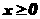 ,求动点
,求动点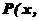 [(
[(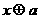 )
)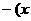
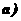 ]1/2)的轨迹C的方程;
]1/2)的轨迹C的方程;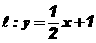 与(1)中的轨迹C交于
与(1)中的轨迹C交于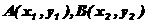 两点,
两点,
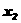 )+(
)+(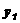
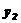 )]1/2=
)]1/2= ,试求
,试求 的值;
的值; (III)设
(III)设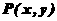 是平面上任意一点,定义
是平面上任意一点,定义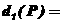 {
{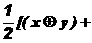
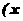
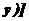 }1/2,
}1/2,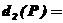 [
[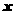
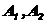 ,使其满足
,使其满足 ,
, (II)存款利率定为多少时,银行可获得最大利益?
(II)存款利率定为多少时,银行可获得最大利益?