0 446135 446143 446149 446153 446159 446161 446165 446171 446173 446179 446185 446189 446191 446195 446201 446203 446209 446213 446215 446219 446221 446225 446227 446229 446230 446231 446233 446234 446235 446237 446239 446243 446245 446249 446251 446255 446261 446263 446269 446273 446275 446279 446285 446291 446293 446299 446303 446305 446311 446315 446321 446329 447348
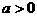 ,函数
,函数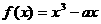 在
在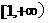 上是单调增函数,则a的最大值是( )
上是单调增函数,则a的最大值是( )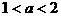 ,
,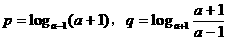 ,则
,则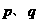 的大小关系是( )
的大小关系是( )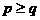 B.
B.
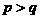 C.
C.
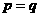 D.
D.
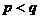
 (4)DN与BN垂直
(4)DN与BN垂直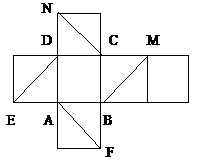
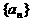 满足
满足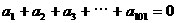 ,则有( )
,则有( ) B.
B.
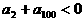
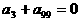 D.
D.
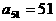
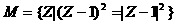 ,则M是( )
,则M是( )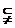 M
M 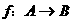 ,其中集合A={
,其中集合A={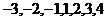 },集合B中的元素都是A中元素在映射f下的象,且对任意的
},集合B中的元素都是A中元素在映射f下的象,且对任意的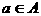 在B中和它对应的元素是| a |,则集合B中元素的个数是( )
在B中和它对应的元素是| a |,则集合B中元素的个数是( )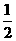 )=-1,且满足x,y∈(-1,1)有f(x)+f(y)=f(
)=-1,且满足x,y∈(-1,1)有f(x)+f(y)=f(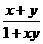 )
)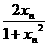 ,求f(xn);
,求f(xn);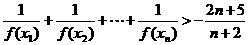
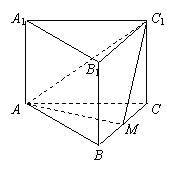 (甲)如图,正三棱柱
(甲)如图,正三棱柱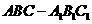 的底面边长为
的底面边长为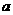 ,点
,点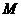 在边
在边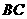 上,
上,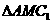 是以点M为直角顶点的等腰直角三角形.
是以点M为直角顶点的等腰直角三角形.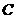 到平面
到平面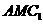 的距离;
的距离; 的大小.
的大小.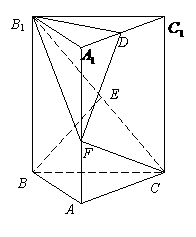 (乙) 如图,直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=
(乙) 如图,直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=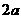 ,BB1=
,BB1=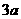 ,D为A1C1的中点,E为B1C的中点,
,D为A1C1的中点,E为B1C的中点,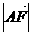 ;若不存在,说明理由.
;若不存在,说明理由. 20.(本小题满分12分)
20.(本小题满分12分)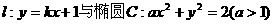 交于A、B
交于A、B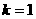 ,且四边形OAPB为矩形,求a的值;
,且四边形OAPB为矩形,求a的值;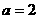 ,当k变化时(k∈R),求点P的轨迹方程.
,当k变化时(k∈R),求点P的轨迹方程.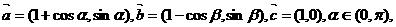
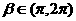 ,
,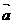 与
与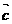 的夹角
的夹角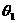 ,
,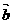 与
与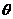 2,且
2,且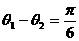 ,求
,求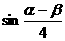 的值。
的值。