(17)若关于x的不等式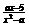 <0的解集为M,
<0的解集为M,
(1)当a=4时,求集合M. (2)若3ÎM且5 ÏM,求实数a的取值范围.
(18)在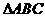 中,a,b,c分别是
中,a,b,c分别是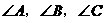 的对边长,已知a,b,c成等比数列,且
的对边长,已知a,b,c成等比数列,且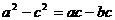 ,求
,求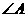 的大小及
的大小及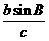 的值。
的值。
(19)已知点A(2,8),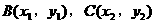 在抛物线
在抛物线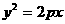 上,
上, 的重心与此抛物线的焦点F重合(如图)
的重心与此抛物线的焦点F重合(如图)
(I)写出该抛物线的方程和焦点F的坐标; (II)求线段BC中点M的坐标;
(III)求BC所在直线的方程。
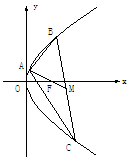
(20)已知某椭圆的焦点是F1(-4,0)、F2(4,0),过点F2并垂直于x轴的直线与椭圆的一个交点为B,且|F1B|+|F2B|=10.椭圆上不同的两点A(x1,y1)、C(x2,y2)满足条件:|F2A|、|F2B|、|F2C|成等差数列.
(I)求该椭圆的方程; (Ⅱ)求弦AC中点的横坐标.
(Ⅲ)设弦AC垂直平分线的方程为y=kx+m,求m的取值范围.
(21)某厂生产某种零件,每个零件的成本为40元,出厂单价定为60元,该厂为鼓励销售商订购,决定当一次订购量超过100个时,每多订购一个,订购的全部零件的出厂单价就降低0.02元,但实际出厂单价不能低于51元。
(I)当一次订购量为多少个时,零件的实际出厂单价恰降为51元?
(II)设一次订购量为x个,零件的实际出厂单价为P元,写出函数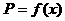 的表达式;
的表达式;
(Ⅲ)当销售商一次订购500个零件时,该厂获得的利润是多少元?如果订购1000个,利润又是多少元?(工厂售出一个零件的利润=实际出厂单价-成本)
(22)下表给出一个“等差数阵”:
|
4 |
7 |
( ) |
( ) |
( ) |
…… |
 |
…… |
|
7 |
12 |
( ) |
( ) |
( ) |
…… |
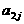 |
…… |
|
( ) |
( ) |
( ) |
( ) |
( ) |
…… |
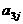 |
…… |
|
( ) |
( ) |
( ) |
( ) |
( ) |
…… |
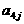 |
…… |
|
…… |
…… |
…… |
…… |
…… |
…… |
…… |
…… |
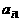 |
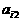 |
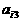 |
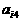 |
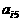 |
…… |
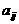 |
…… |
|
…… |
…… |
…… |
…… |
…… |
…… |
…… |
…… |
其中每行、每列都是等差数列,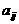 表示位于第i行第j列的数。
表示位于第i行第j列的数。
(I)写出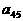 的值; (II)写出
的值; (II)写出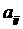 的计算公式;
的计算公式;
(III)证明:正整数N在该等差数列阵中的充要条件是2N+1可以分解成两个不是1的正整数之积。
高三第二学期数学练习卷
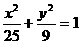 上到两个焦点距离之积最小的点的坐标是________________。
上到两个焦点距离之积最小的点的坐标是________________。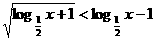 的解集为________________。
的解集为________________。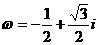 对应的向量为
对应的向量为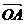 ,复数
,复数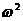 对应的向量为
对应的向量为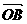 。那么向量
。那么向量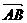 对应的复数是()
对应的复数是()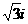 (D)
(D)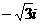
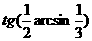 的值为()
的值为()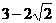 (B)
(B)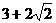
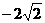 (D)
(D)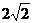
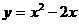 的定义域为{0,1,2,3},那么其值域为()
的定义域为{0,1,2,3},那么其值域为()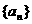 中,
中,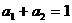 ,
,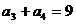 ,那么
,那么 等于()
等于()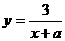 的图象C向左平移一个单位后,得到y=f(x)的图象
的图象C向左平移一个单位后,得到y=f(x)的图象 ,若曲线
,若曲线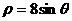 相切的一条直线的方程是()
相切的一条直线的方程是()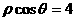 (B)
(B)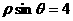
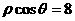 (D)
(D)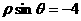
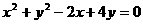 截得的最长弦所在的直线方程是()
截得的最长弦所在的直线方程是() ,点A、B∈平面α,点C∈平面β,且A、B、C均不在直线l上。给出四个命题:
,点A、B∈平面α,点C∈平面β,且A、B、C均不在直线l上。给出四个命题: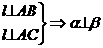 ②
②
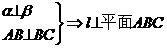 ④
④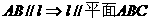
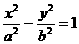 (a>0,b>0)的实轴长、虚轴长、焦距依次成等差数列。那么这个双曲线的离心率e等于()
(a>0,b>0)的实轴长、虚轴长、焦距依次成等差数列。那么这个双曲线的离心率e等于()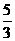 (D)
(D)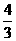
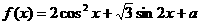 (a为实常数)在区间
(a为实常数)在区间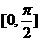 上的最小值为-4,那么a的值等于()
上的最小值为-4,那么a的值等于()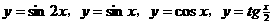 中,最小正周期为
中,最小正周期为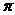
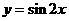 B.
B.
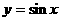 C.
C. 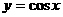 D.
D. 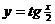
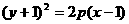 B.
B.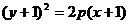
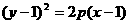 D.
D.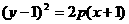
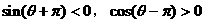 ,则下列不等关系中必定成立的是 ( )
,则下列不等关系中必定成立的是 ( )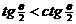 B.
B. 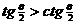 C.
C. 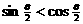 D.
D. 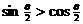
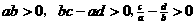 (其中a,b,c,d均
(其中a,b,c,d均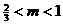 时,复数
时,复数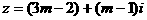 在复平面上对应的点位于 象限。
在复平面上对应的点位于 象限。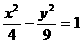 的渐近线方程是 。
的渐近线方程是 。 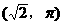 且过极点的圆的方程为
。
且过极点的圆的方程为
。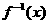 为函数
为函数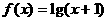 的反函数,则
的反函数,则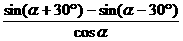 的值为____________。
的值为____________。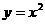 上的点P与A(0,-4)和点B(2,0)构成的△PAB的面积最小,P点的坐标应为 .
上的点P与A(0,-4)和点B(2,0)构成的△PAB的面积最小,P点的坐标应为 .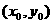 在直线
在直线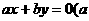 、
、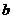 为常数)上,则
为常数)上,则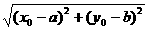 的最小值为
.
的最小值为
.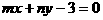 与圆
与圆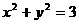 没有公共点,则以(m,n)为点P的坐标,过点P的一条直线与椭圆
没有公共点,则以(m,n)为点P的坐标,过点P的一条直线与椭圆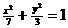 的点有______个。
的点有______个。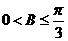 ;
;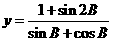 的取值范围。
的取值范围。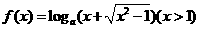 。
。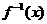 ;
;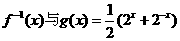 的大小。
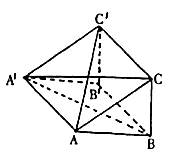
的大小。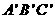 中,四边形
中,四边形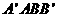 是菱形,四边形
是菱形,四边形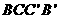 是矩形,
是矩形,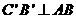 。
。
 。现有3万元资金投入经营甲、乙两种商品,为获得最大利润,对甲、乙两种商品的资金投入分别是多少?
。现有3万元资金投入经营甲、乙两种商品,为获得最大利润,对甲、乙两种商品的资金投入分别是多少?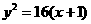 的焦点为其右焦点,并且椭圆的长轴长、短轴长、焦距成等差数列,A、B是椭圆上两点,弦AB中点M在直线x=4上。
的焦点为其右焦点,并且椭圆的长轴长、短轴长、焦距成等差数列,A、B是椭圆上两点,弦AB中点M在直线x=4上。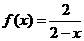 ,记数列
,记数列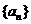 的前n项和为
的前n项和为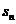 ,且有
,且有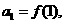 当
当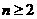 时,
时,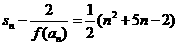 。
。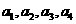 ;
;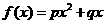 ,其中p>0,p+q>1,对于数列
,其中p>0,p+q>1,对于数列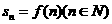 。
。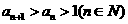 ;
;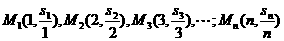 在同一直线
在同一直线 上;
上;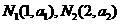 作直线
作直线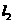 的夹角为
的夹角为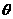 ,求
,求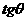 的最大值。
的最大值。
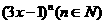 的展形式中各项系数的和为128,则展开式中
的展形式中各项系数的和为128,则展开式中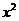 项的系数为____________。
项的系数为____________。 是正实数,如果函数
是正实数,如果函数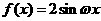 在
在 上是增函数,那么
上是增函数,那么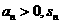 是它的前n项和,且
是它的前n项和,且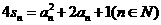 ,则它的通项公式是
,则它的通项公式是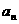 =______________________。
=______________________。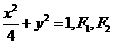 是它的两个焦点,若P是椭圆上任意一点,
是它的两个焦点,若P是椭圆上任意一点,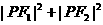 的最小值是________________。
的最小值是________________。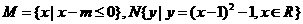 ,若
,若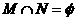 ,则实数m的取值范围是( )
,则实数m的取值范围是( )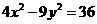 只有一个公共点,则这样的直线有( )
只有一个公共点,则这样的直线有( )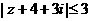 中的复数z的模应满足的不等式是( )
中的复数z的模应满足的不等式是( )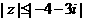
 (D)
(D)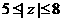
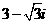 对应的向量按顺时针方向旋转
对应的向量按顺时针方向旋转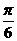 ,所得向量对应的复数是( )
,所得向量对应的复数是( )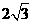 (B)
(B)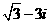
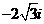 (D)
(D)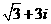
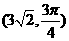
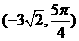
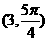
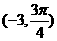
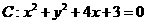 上任意一点,则
上任意一点,则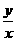 的取值范围是
的取值范围是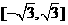 (B)
(B)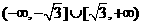
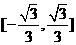 (D)
(D)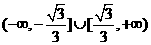
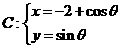 (
( )上任意一点,则
)上任意一点,则 ,则f(x)的反函数
,则f(x)的反函数 的图象是( )
的图象是( )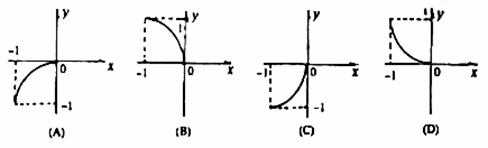
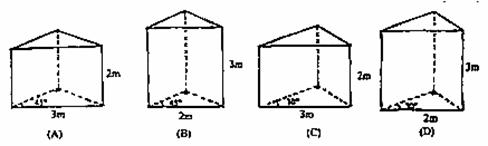
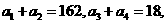 那么
那么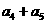 等于( )
等于( )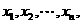 有:
有: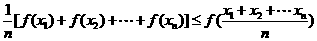 ”
”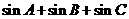 的最大值是( )
的最大值是( )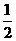 (B)
(B)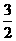
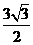 (D)
(D)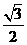
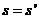 (B)
(B)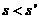
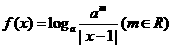 ,则f(-1) 与f (π)的大小关系是( )
,则f(-1) 与f (π)的大小关系是( )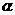 、
、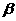 为方程x2-x-1=0的根,且
为方程x2-x-1=0的根,且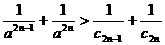
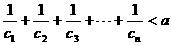
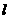 ,使
,使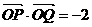 ?若存在,求出直线
?若存在,求出直线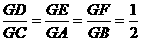 。
。