摘要:在△ABC中.角A.B.C所对的边分别为a,b,c.若a,b,c成等比数列. (Ⅰ)求证, (Ⅱ)求的取值范围. 已知a>1.. 的反函数, (Ⅱ)试比较的大小. 的定义域, 的反函数, (Ⅲ)试比较的大小. (文)如图.在三棱柱ABC-中.四边形是菱形.四边形是矩形.. (Ⅰ)求证:平面CA′B⊥平面A′AB, (Ⅱ)若C′B′=3.AB=4.∠ABB′=60°.求直线AC′与平面BCC′所成角的正弦值. (理)如图.在三棱柱ABC-中.四边形是菱形.四边形是矩形..且C′B′=3.AB=4.∠ABB′=60°. (Ⅰ)求证:平面CA′B⊥平面A′AB, (Ⅱ)求直线AC′与平面BCC′所成角的大小 (Ⅲ)求三棱锥A′BCC′的体积. (文)有甲.乙两种商品.经营销售这两种商品所能获得的利润依次为P万元和Q万元.它们与投入资金x的关系有经验公式.现有3万元资金投入经营甲.乙两种商品.为获得最大利润.对甲.乙两种商品的资金投入分别是多少? (理)有甲.乙两种商品.经营销售这两种商品所能获得的利润依次为P万元和Q万元.它们与投入资金x的关系有经验公式.现有a万元资金投入经营甲.乙两种商品.为获得最大利润.对甲.乙两种商品的资金投入分别是多少? 已知椭圆中心在原点.以抛物线的焦点为其右焦点.并且椭圆的长轴长.短轴长.焦距成等差数列.A.B是椭圆上两点.弦AB中点M在直线x=4上. (Ⅰ)求椭圆方程, (Ⅱ)求证弦AB的重直平分线l与x轴交于定点. 求直线l的斜率的取值范围. (文)已知函数.记数列的前n项和为.且有当时.. (Ⅰ)计算, (Ⅱ)求出数列的通项公式.并给予证明. (理)已知函数.其中p>0,p+q>1.对于数列.设它的前n项和为.且满足. (Ⅰ)求数列的通项公式.并证明, (Ⅱ)求证:点在同一直线上, (Ⅲ)若过点作直线的夹角为.求的最大值.
网址:http://m.1010jiajiao.com/timu3_id_4462275[举报]
 、
、 、
、 ,且满足
,且满足 .
. ,求
,求 的最小值.
的最小值. 、
、 、
、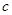 ,且满足
,且满足 .
. ,求
,求 的最小值.
的最小值.