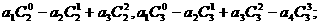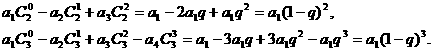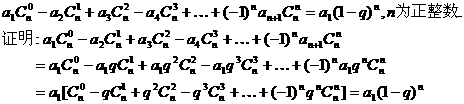0 446099 446107 446113 446117 446123 446125 446129 446135 446137 446143 446149 446153 446155 446159 446165 446167 446173 446177 446179 446183 446185 446189 446191 446193 446194 446195 446197 446198 446199 446201 446203 446207 446209 446213 446215 446219 446225 446227 446233 446237 446239 446243 446249 446255 446257 446263 446267 446269 446275 446279 446285 446293 447348
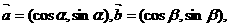 则
则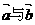 一定满足( )
A.
一定满足( )
A.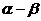 B.
B.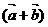 ⊥
⊥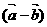
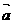 ∥
∥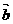 D.
D.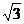 +i,则z=
+i,则z=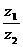 在复平面内对应点位于( )
在复平面内对应点位于( )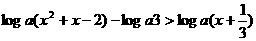 (a>0,a≠1)。
(a>0,a≠1)。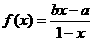 (x≠1,a>b)。
(x≠1,a>b)。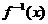 ;
;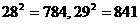 )。
)。
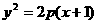 (p >0),直线l:x+y=m过抛物线的焦点F且被抛物线截得的弦长为3。
(p >0),直线l:x+y=m过抛物线的焦点F且被抛物线截得的弦长为3。 和
和 分别表示数列
分别表示数列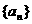 和
和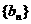 的前n项的和,对任意正整数n,
的前n项的和,对任意正整数n,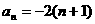 ,
,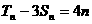 。
。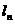 的斜率为
的斜率为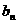 ,且与曲线
,且与曲线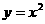 有且仅有一个交点,与y轴交于点
有且仅有一个交点,与y轴交于点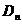 ,记
,记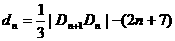 ,求
,求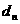 ;
;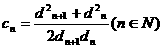 ,求证:
,求证: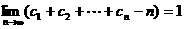 。
。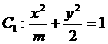 与
与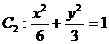 有相同的离心率e,那么m的值为___________.
有相同的离心率e,那么m的值为___________.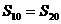 ,则
,则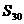 的值是_________。
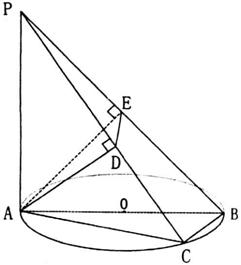
的值是_________。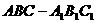 中,P、Q分别是侧棱
中,P、Q分别是侧棱 、
、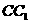 上的点,且
上的点,且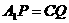 ,则四棱锥
,则四棱锥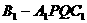 的体积与多面体
的体积与多面体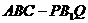 的体积的比值为________。
的体积的比值为________。
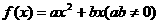 ,若
,若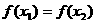 ,且
,且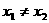 ,那么
,那么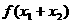 的值是_______________。
的值是_______________。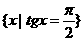
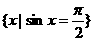
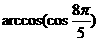 的值是
的值是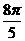 (B)
(B)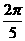
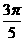 (D)
(D)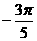
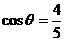 ,
,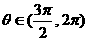 ,那么ctgθ的值等于
,那么ctgθ的值等于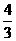 (B)
(B)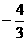
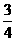 (D)
(D)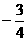
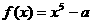 ,且f(-1)=0,那么
,且f(-1)=0,那么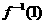 的值是
的值是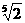
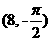 ,(8,
,(8,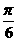 ),那么线段AB的中点C的极坐标可以是
),那么线段AB的中点C的极坐标可以是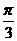 ) (B)(4,
) (B)(4,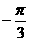 )
)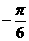 ) (D)(4,
) (D)(4,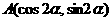 ,
,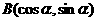 ,则A,B两点间的距离为
,则A,B两点间的距离为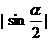 (B)
(B)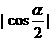
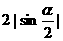 (D)
(D)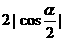
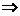 b⊥a (B)b⊥a
b⊥a (B)b⊥a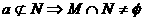
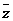 满足
满足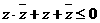 ,
,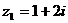 ,则
,则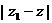 的最大值是
的最大值是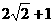 (B)
(B)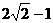
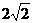 (C)2
(C)2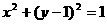 上任意一点时,不等式m+n+c≥0恒成立,则c的取值范围是
上任意一点时,不等式m+n+c≥0恒成立,则c的取值范围是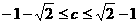 (B)
(B)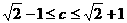
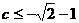 (D)
(D)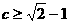
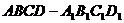 是棱长为a的正方体,P是
是棱长为a的正方体,P是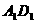 上的定点,Q是
上的定点,Q是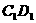 上的动点,长为b(b是常数,0 < b < a)的线段EF在棱AB上滑动,那么四面体PQEF的体积是
上的动点,长为b(b是常数,0 < b < a)的线段EF在棱AB上滑动,那么四面体PQEF的体积是 为正整数.
为正整数. ;
;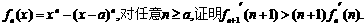
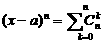
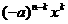 ,
,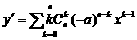
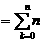
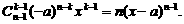
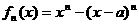 求导数:
求导数: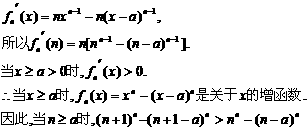
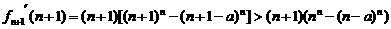
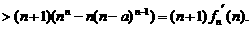
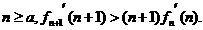
 元;设全年运输和保管总费用为y元,则
元;设全年运输和保管总费用为y元,则 。
。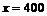 时,
时,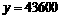 ,代入上式解之得
,代入上式解之得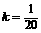
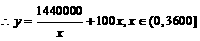
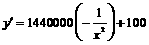 ,令
,令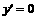 ,解之得
,解之得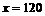 (台)
(台)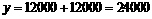 (元)
(元)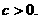 设
设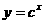 在R上单调递减.
在R上单调递减.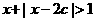 的解集为R,如果P和Q有且仅有一个正确,求
的解集为R,如果P和Q有且仅有一个正确,求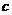 的取值范围.
的取值范围.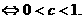
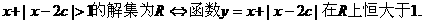

 ,求函数
,求函数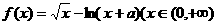 的单调区间.
的单调区间.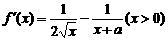 .
. 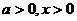 时
时 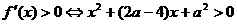 .
.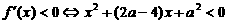
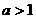 时,对所有
时,对所有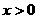 ,有
,有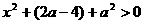 .
.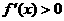 ,此时
,此时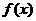 在
在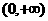 内单调递增.
内单调递增.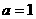 时,对
时,对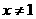 ,有
,有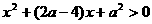 ,
, )内单调递增
)内单调递增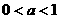 时,令
时,令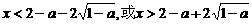 .
.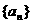 (n为正整数)是首项是a1,公比为q的等比数列.
(n为正整数)是首项是a1,公比为q的等比数列.