0 446060 446068 446074 446078 446084 446086 446090 446096 446098 446104 446110 446114 446116 446120 446126 446128 446134 446138 446140 446144 446146 446150 446152 446154 446155 446156 446158 446159 446160 446162 446164 446168 446170 446174 446176 446180 446186 446188 446194 446198 446200 446204 446210 446216 446218 446224 446228 446230 446236 446240 446246 446254 447348
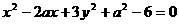 的一个焦点在直线
的一个焦点在直线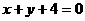 上,则
上,则 ( C )
( C ) 和
和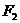 为双曲线
为双曲线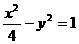 的两个焦点,点
的两个焦点,点 在双曲线上且满足
在双曲线上且满足 ,则△
,则△ 的面积是___1___.
的面积是___1___.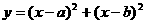 (
( 、
、 为常数)的最小值为( B
)
为常数)的最小值为( B
) C.
C. D.最小值不存在
D.最小值不存在 的两根
的两根 、
、 ,且点
,且点 +y
+y __.
__. 的单调递增区间是( D
)
的单调递增区间是( D
) B.
B.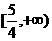 C.
C. D.
D.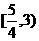
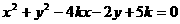 表示圆的充要条件是___
表示圆的充要条件是___ ____.
____.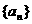 中,
中,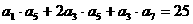 ,则
,则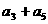 =___5___.
=___5___.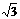 B.
B.  C. 5
D. 6
C. 5
D. 6 ,由已知“长方体的全面积为11,其12条棱的长度之和为24”而得:
,由已知“长方体的全面积为11,其12条棱的长度之和为24”而得: .
.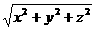 =
=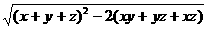 =
=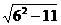 =5,所以选B.
=5,所以选B. 的两实根为
的两实根为 、
、 ,若(
,若(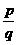 )
) )
) 的取值范围.
的取值范围.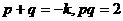 ,
,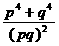 =
=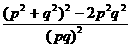 =
=
 ≤7, 解得
≤7, 解得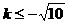 或
或 .
.
 或
或 ,
, 或
或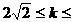
 .
. ,给定
,给定 、
、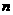
 ,且满足
,且满足 ,
,  ;
;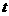 ,使当
,使当 时,
时, ?若不存在,说出理由;若存在,指出
?若不存在,说出理由;若存在,指出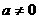 且
且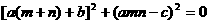 ,
, 即
即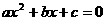 的两根,且
的两根,且 ,所以,
,所以, 时,
时,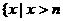 或
或 ;
;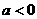 时,
时,  ,
,  ,则
,则 ,即
,即 若
若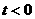 ,则
,则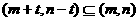 ,不满足对所有的
,不满足对所有的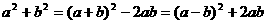 ;
;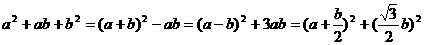 ;
;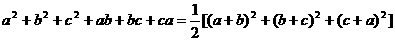 .
.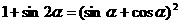 ;
; ;…… 等等.
;…… 等等. 的离心率是
的离心率是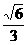 ,F是其左焦点,若直线
,F是其左焦点,若直线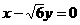 与椭圆交于AB两点,且
与椭圆交于AB两点,且 ,求该椭圆的方程。
,求该椭圆的方程。