0 445299 445307 445313 445317 445323 445325 445329 445335 445337 445343 445349 445353 445355 445359 445365 445367 445373 445377 445379 445383 445385 445389 445391 445393 445394 445395 445397 445398 445399 445401 445403 445407 445409 445413 445415 445419 445425 445427 445433 445437 445439 445443 445449 445455 445457 445463 445467 445469 445475 445479 445485 445493 447348
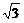 ,BC=a,又PA⊥平面ABCD,PA=4.
(1)若在边BC上存在一点Q,使PQ⊥QD,求a的取值范围;
(2)当BC上存在唯一点Q,使PQ⊥QD时,求异面直线AQ与PD所成角的大小;
(3)若a=4,且PQ⊥QD,求二面角A-PD-Q的大小.
,BC=a,又PA⊥平面ABCD,PA=4.
(1)若在边BC上存在一点Q,使PQ⊥QD,求a的取值范围;
(2)当BC上存在唯一点Q,使PQ⊥QD时,求异面直线AQ与PD所成角的大小;
(3)若a=4,且PQ⊥QD,求二面角A-PD-Q的大小.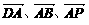 为x、y、z轴建立空间直角坐标系,则
为x、y、z轴建立空间直角坐标系,则 =(t,
=(t,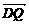 =(t+a,
=(t+a, =0 即t2+at+3=0 ①
∴△=a2-12≥0 Þ a≥2
=0 即t2+at+3=0 ①
∴△=a2-12≥0 Þ a≥2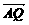 =(-
=(-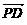 =(-2
=(-2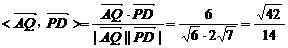 故异面直线AQ与PD所成角为arccos
故异面直线AQ与PD所成角为arccos .
. 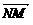 =(t-m,0,-n),
=(t-m,0,-n),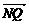 =(t-m,
=(t-m,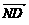 =(-4-m,0,-n) ∵MN⊥PD,ND、PD共线,∴
=(-4-m,0,-n) ∵MN⊥PD,ND、PD共线,∴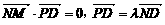
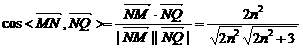
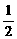 t
t 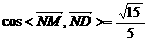 ,当t=-3时,
,当t=-3时,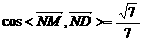
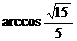 或
或 .
.
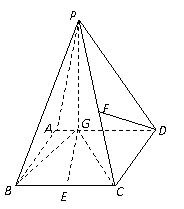 如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在AD上,且PG=4,
如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在AD上,且PG=4,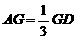 ,BG⊥GC,GB=GC=2,E是BC的中点.
,BG⊥GC,GB=GC=2,E是BC的中点.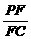 的值.
的值.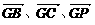 为x轴、y轴、z轴建立空间直角坐标系,
为x轴、y轴、z轴建立空间直角坐标系,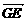 =(1,1,0),
=(1,1,0), =(0,2,4)
=(0,2,4) 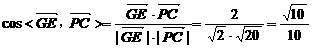
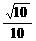 .
.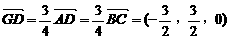
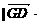 n |=
n |=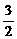
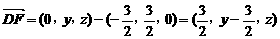
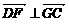 ,∴
,∴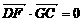 , 即
, 即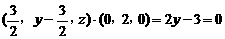 ,∴
,∴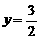 又
又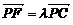 ,即(0,
,即(0,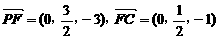 ,∴
,∴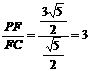
 的棱
的棱 的中点,则点C到 平面
的中点,则点C到 平面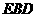 的距离等于
。
的距离等于
。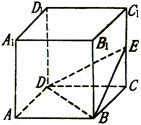 一个正方体的棱长为2,将八个直径各为1的球放进去之后,正中央空间能放下的最大的球的直径为
.
一个正方体的棱长为2,将八个直径各为1的球放进去之后,正中央空间能放下的最大的球的直径为
.
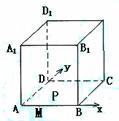 如图,正方体ABCD-A1B1C1D1的棱长为1,点M在棱AB上,且AM=
如图,正方体ABCD-A1B1C1D1的棱长为1,点M在棱AB上,且AM=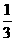 ,点P在平 面ABCD上,且动点P到直线A1D1的距离的平方与P到点M的距离的平方的差为1,在xAy直角坐标系中,动点P的轨迹方程是
.
,点P在平 面ABCD上,且动点P到直线A1D1的距离的平方与P到点M的距离的平方的差为1,在xAy直角坐标系中,动点P的轨迹方程是
.
 ,则此正三棱锥的外接球的表面积为
,则此正三棱锥的外接球的表面积为
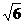 , 则半球
, 则半球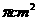 B.14
B.14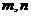 都平行于平面
都平行于平面 ,则
,则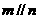
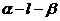 是直二面角,若直线
是直二面角,若直线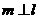 ,则
,则
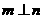 ,则
,则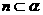 或
或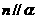
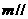 平面
平面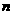 与
与