0 445336 445344 445350 445354 445360 445362 445366 445372 445374 445380 445386 445390 445392 445396 445402 445404 445410 445414 445416 445420 445422 445426 445428 445430 445431 445432 445434 445435 445436 445438 445440 445444 445446 445450 445452 445456 445462 445464 445470 445474 445476 445480 445486 445492 445494 445500 445504 445506 445512 445516 445522 445530 447348
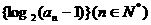 为等差数列,且
为等差数列,且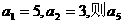 等于 ( )
等于 ( )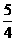 B.-3 C.1 D.5
B.-3 C.1 D.5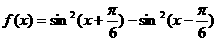 是 ( )
是 ( )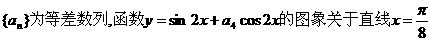 对称,则数列
对称,则数列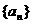 的前7项和S7等于 ( )
的前7项和S7等于 ( )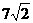 B.-
B.-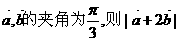 等于 ( )
等于 ( )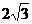 B.3 C.
B.3 C.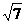 D.
D.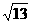
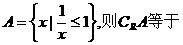 ( )
( )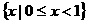 B.
B.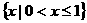
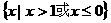 D.
D.
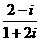 等于 ( )
等于 ( )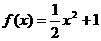 ,则过曲线
,则过曲线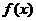 上的点(2,3)的切线方程为
上的点(2,3)的切线方程为
 14,若椭圆
14,若椭圆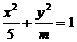 的离心率
的离心率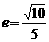 ,则
,则 的值是
的值是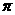 ,则
球的表面积是
,则
球的表面积是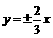 ,经过点
,经过点 ,求曲线的的标准方程。
,求曲线的的标准方程。
 ?若存在,求出直线L的方程;若不存在,说明理由。
?若存在,求出直线L的方程;若不存在,说明理由。


 (1)求证:DM//平面PAC;
(1)求证:DM//平面PAC;

 (2)求证:平面PAC⊥平面ABC;
(2)求证:平面PAC⊥平面ABC;
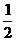 ,且它的一个焦点与抛物线y2=4x的焦点重合。
,且它的一个焦点与抛物线y2=4x的焦点重合。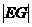 是否为定值?为什么?
是否为定值?为什么?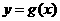 与
与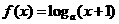 (
(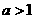 )的图象关于原点对称。
)的图象关于原点对称。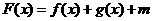 为奇函数,试确定实数
为奇函数,试确定实数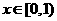 时,总有
时,总有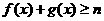 成立,求实数
成立,求实数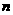 的取值范围。
的取值范围。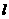 经过点
经过点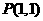 ,倾斜角
,倾斜角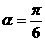 ,
,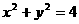 相交与两点
相交与两点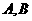 ,求点
,求点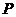 到
到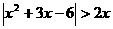
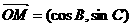 ,
, .
.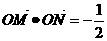 ,求角A大小;
,求角A大小; 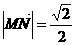 ,求
,求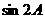 .
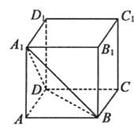
.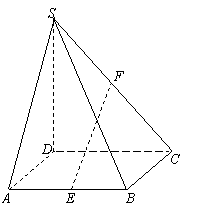 如图,在四棱锥S-ABCD中,底面ABCD为正方形,侧棱SD⊥底面ABCD,E、F分别是AB、SC的中点.
如图,在四棱锥S-ABCD中,底面ABCD为正方形,侧棱SD⊥底面ABCD,E、F分别是AB、SC的中点.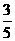 ;若仅通过面试而笔试不通过,则被确认为通过自主招生的可能性为
;若仅通过面试而笔试不通过,则被确认为通过自主招生的可能性为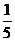 ;两者均不通过,则淘汰。现知有一报考该校自主招生的学生在推荐材料审核,笔试,面试这三环节中通过的概率分别为
;两者均不通过,则淘汰。现知有一报考该校自主招生的学生在推荐材料审核,笔试,面试这三环节中通过的概率分别为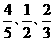 ,假设各环节之间互不影响.试求:
,假设各环节之间互不影响.试求: 中,
中,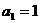 ,其前
,其前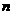 项和
项和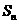 满足:
满足:
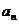 ;
;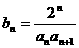 ,数列
,数列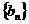 前项的和为
前项的和为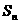 ,求证:
,求证: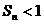
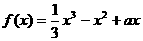 ,
,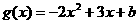 ,当
,当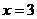 时,
时,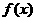 取得极值.
取得极值.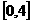 上的最大值与最小值.
上的最大值与最小值.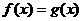 解的个数.
解的个数.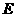 中心在坐标原点,焦点在坐标轴上,且经过
中心在坐标原点,焦点在坐标轴上,且经过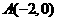 、
、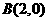 、
、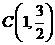 三点.
三点.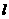 与椭圆
与椭圆 、
、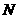 两点,
两点,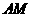 与
与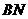 所在的直线交于点Q.
所在的直线交于点Q.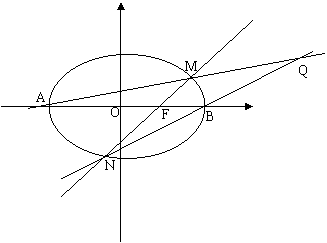 (2)是否存在这样直线
(2)是否存在这样直线 ,使得点Q恒在直线
,使得点Q恒在直线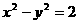 的双曲线离心率为:
的双曲线离心率为:
 10:为了调查某厂工人生产某种产品的能力,随机抽查了20位工人某天生产该产品的数量.产品数量的分组区间为
10:为了调查某厂工人生产某种产品的能力,随机抽查了20位工人某天生产该产品的数量.产品数量的分组区间为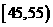 ,
,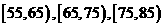 ,
, 由此得到频率分布直方图如下图,则这20名工人中一天生产该产品数量在
由此得到频率分布直方图如下图,则这20名工人中一天生产该产品数量在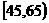 的人数大约是
的人数大约是
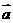 与
与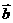 的夹角为,则称向量“
的夹角为,则称向量“
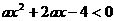 的解集为R,则实数
的解集为R,则实数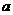 取值范围为
取值范围为
 14:若实数
14:若实数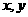 满足:
满足: 表示的区域的面积为
表示的区域的面积为
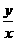 的取值范围是
的取值范围是
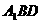 的距离为
,若P为线段
的距离为
,若P为线段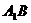 上一个动点,则
上一个动点,则 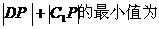
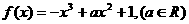
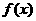 的图象上横坐标为
的图象上横坐标为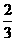 的点处存在垂直于y 轴的切线,求a 的值;
的点处存在垂直于y 轴的切线,求a 的值; 的
的