0 445342 445350 445356 445360 445366 445368 445372 445378 445380 445386 445392 445396 445398 445402 445408 445410 445416 445420 445422 445426 445428 445432 445434 445436 445437 445438 445440 445441 445442 445444 445446 445450 445452 445456 445458 445462 445468 445470 445476 445480 445482 445486 445492 445498 445500 445506 445510 445512 445518 445522 445528 445536 447348
 ,
, 。规定:给定一个实数
。规定:给定一个实数 ,赋值
,赋值 ,若
,若 ,则继续赋值
,则继续赋值 ,…,以此类推,若
,…,以此类推,若 ,则
,则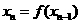 ,否则停止赋值,如果得到
,否则停止赋值,如果得到 称为赋值了
称为赋值了 次(
次( )。已知赋值
)。已知赋值 次后该过程停止,则
次后该过程停止,则 B.
B.
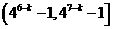 D.
D.
 ,
, ,
,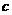 均为正数,且
均为正数,且 ,
, ,
, ,则( )
,则( ) B.
B. C.
C. D.
D.
 -
- ,且当二次方程
,且当二次方程 无实根时的
无实根时的 ( )
( )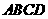 的外接球球心在
的外接球球心在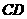 上,且
上,且 ,
, ,则在外接球球面上
,则在外接球球面上 ,
, 两点间的球面距离是( )
两点间的球面距离是( )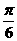 B.
B. C.
C. D.
D.
 中,已知
中,已知 顶点
顶点 和
和 ,顶点
,顶点 上,则
上,则 的值是( )
的值是( ) B.
B. C.
C. D.与点
D.与点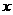 ,有
,有 ,
, ,且
,且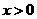 时,
时, ,
, ,则
,则 时,有( )
时,有( )
 ,
, 中,若
中,若 ,则
,则 ( )
( ) B.
B.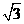 C.
C.
 ,若
,若 ,
, ,则
,则 等于( )
等于( )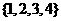 B.
B. C.
C. D.
D.
 的前
的前 项和为
项和为 ,对一切
,对一切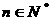 ,点
,点 都在函数
都在函数 的图像上。
的图像上。
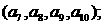
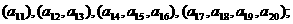
 分别计算各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列
分别计算各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列 ,求
,求
 为数列
为数列 的前
的前 ,使得不等式
,使得不等式 对一切
对一切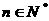 都成立?若存在,求出
都成立?若存在,求出 ----------------------------4分
----------------------------4分 ,所以数列
,所以数列 依次按1项、2项、3项、4项循环地分为(2),(4,6),(8,10,12),(14,16,18,20);(22),(24,26),(28,30,32),(34,36,38,40);(42),….每一次循环记为一组.由于每一个循环含有4个括号,故
依次按1项、2项、3项、4项循环地分为(2),(4,6),(8,10,12),(14,16,18,20);(22),(24,26),(28,30,32),(34,36,38,40);(42),….每一次循环记为一组.由于每一个循环含有4个括号,故 是第25组中第4个括号内各数之和.由分组规律知,由各组第4个括号中所有第1个数组成的数列是等差数列,且公差为20.同理,由各组第4个括号中所有第2个数、所有第3个数、所有第4个数分别组成的数列也都是等差数列,且公差均为20.故各组第4个括号中各数之和构成等差数列,且公差为80.注意到第一组中第4个括号内各数之和是68,所以
是第25组中第4个括号内各数之和.由分组规律知,由各组第4个括号中所有第1个数组成的数列是等差数列,且公差为20.同理,由各组第4个括号中所有第2个数、所有第3个数、所有第4个数分别组成的数列也都是等差数列,且公差均为20.故各组第4个括号中各数之和构成等差数列,且公差为80.注意到第一组中第4个括号内各数之和是68,所以 =22,所以
=22,所以 =2010.-------------8分
=2010.-------------8分 ,故
,故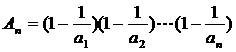 ,
, .
. ,
, 对一切
对一切 都成立,就是
都成立,就是 对一切
对一切 ,则只需
,则只需 即可.
即可. ,
, ,故
,故 是单调递减,于是
是单调递减,于是 .
. ,即
,即 ,
, ,或
,或 .
. .-------------------------------------------------------12分
.-------------------------------------------------------12分 及双曲线方程
及双曲线方程 可得点
可得点 直线
直线 方程是
方程是
 且
且 在直线
在直线
 ①
① 的垂直平分线方程为
的垂直平分线方程为 ②
② P是△ABC的外接圆圆心,
P是△ABC的外接圆圆心, 点P的坐标
点P的坐标 满足方程①和②
满足方程①和② 得
得
 ---------------------------------------------------------6分
---------------------------------------------------------6分 和
和 的斜率存在且不为零,设
的斜率存在且不为零,设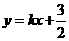 ,
, ,
,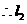 的方程为
的方程为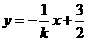
 ------------------------------8分
------------------------------8分 直线
直线 ,则
,则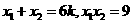 。
。

 -----------------10分
-----------------10分 ,即
,即 时,等号成立。
时,等号成立。