摘要:如图.在矩形ABCD中.AB=.BC=a.又PA⊥平面ABCD.PA=4. (1)若在边BC上存在一点Q.使PQ⊥QD.求a的取值范围, (2)当BC上存在唯一点Q.使PQ⊥QD时.求异面直线AQ与PD所成角的大小, (3)若a=4.且PQ⊥QD.求二面角A-PD-Q的大小. 解: (1).以为x.y.z轴建立空间直角坐标系.则 B(0..0).C(-a..0).D(-a.0.0).P 设Q(t..0).则 =(t..-4).=(t+a..0) ∵PQ⊥QD.∴=0 即t2+at+3=0 ① ∴△=a2-12≥0 Þ a≥2. (2).∵BC上存在唯一点Q.使PQ⊥QD. ∴△=a2-12=0 Þ a=2.t=- =(-..0) .=(-2.0.-4) ∴cos 故异面直线AQ与PD所成角为arccos. (3).过Q作QM∥CD交AD于M.则QM⊥AD.M ∵PA⊥平面ABCD.∴PA⊥QM.又QM⊥AD.∴QM⊥平面PAD 过M作MN⊥PD于N.连结NQ.由三垂线定理知QN⊥PD ∴∠MNQ是二面角A-PD-Q的平面角 设N .则=.=(t-m..-n) = ∵MN⊥PD.ND.PD共线.∴ 得:m+n-t=0.m-n=4 ② 由①得:t=-1或t=-3.由②得:n=2+t 当t=-1时..当t=-3时. ∴二面角A-PD-Q的大小为或.
网址:http://m.1010jiajiao.com/timu3_id_4453970[举报]
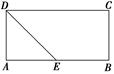
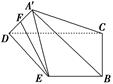
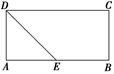
如图,在矩形ABCD中,AB=4,AD=2,E为AB的中点,现将△ ADE沿直线DE翻折成△A′DE,使平面A′DE⊥平面BCDE,F为线段A′D的中点.
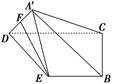
(1)求证:EF//平面A′BC;
(2)求直线A′B与平面A′DE所成角的正切值.
查看习题详情和答案>>
如图,在矩形ABCD中,AB=4,AD=2,E为AB的中点,现将△ ADE沿直线DE翻折成△A′DE,使平面A′DE⊥平面BCDE,F为线段A′D的中点.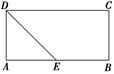
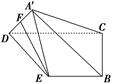
(1)求证:EF//平面A′BC;
(2)求直线A′B与平面A′DE所成角的正切值.
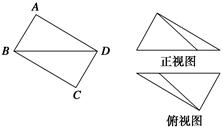
如图,在矩形ABCD中,AB=2,BC=3,沿BD将矩形ABCD折叠,连接AC,所得三棱锥A?BCD正视图和俯视图如图,则三棱锥A?BCD侧视图的面积为( ).
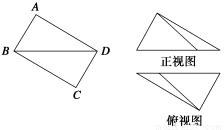
A.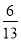 B.
B.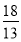 C.
C.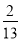 D.
D.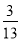
查看习题详情和答案>>