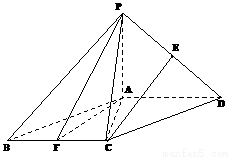
摘要：如图四棱锥P-ABCD中.底面ABCD是平行四边形.PG⊥平面ABCD.垂足为G.G在AD上.且PG＝4..BG⊥GC.GB＝GC＝2.E是BC的中点． (1)求异面直线GE与PC所成的角, (2)求点D到平面PBG的距离, (3)若F点是棱PC上一点.且DF⊥GC.求的值． 解:(1)解:以G点为原点.为x轴.y轴.z轴建立空间直角坐标系. 则B.C.P. 故E ＝. ＝ ∴GE与PC所成的角为arccos． (2)解:平面PBG的单位法向量n＝ ∵ ∴点D到平面PBG的距离为n |＝ (3)解:设F(0.y.z).则 ∵.∴. 即.∴ 又.即(0..z-4)＝λ.∴z=1. 故F(0..1) .∴
网址：http://m.1010jiajiao.com/timu3_id_4453969[举报]
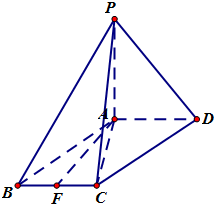如图四棱锥P-ABCD中，底面ABCD是平行四边形，∠ACB=90°，PA⊥平面ABCD，F是BC的中点．（1）求证：DA⊥平面PAC；
（2）试在线段PD上确定一点G，使CG∥平面PAF，并说明理由．
如图四棱锥P-ABCD中，底面ABCD是平行四边形，PG⊥平面ABCD，垂足为G，G在AD上，且PG=4，AG=| 1 |
| 3 |
（1）求异面直线GE与PC所成的角的余弦值；
（2）求点D到平面PBG的距离；
（3）若F点是棱PC上一点，且DF⊥GC，求
| PF |
| FC |
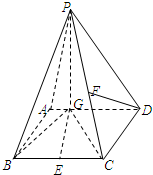
如图四棱锥P-ABCD中，底面ABCD是平行四边形，PC⊥平面ABCD，F是DC的中点，| AE |
| EP |
（Ⅰ）试判断直线EF与平面PBC的位置关系，并予以证明；
（Ⅱ）若四棱锥P-ABCD体积为
| 8 |
| 3 |
| 2 |
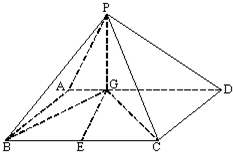如图四棱锥P-ABCD中，底面ABCD是平行四边形，PG⊥平面ABCD，垂足为G，G在AD上且AG=
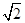,E、F分别为线段PD和BC的中点．