0 445280 445288 445294 445298 445304 445306 445310 445316 445318 445324 445330 445334 445336 445340 445346 445348 445354 445358 445360 445364 445366 445370 445372 445374 445375 445376 445378 445379 445380 445382 445384 445388 445390 445394 445396 445400 445406 445408 445414 445418 445420 445424 445430 445436 445438 445444 445448 445450 445456 445460 445466 445474 447348
 与
与 垂直,垂足为
垂直,垂足为 ,则
,则 的值为( )
的值为( ) ,…
,… ,…
,… ,特别地,
,特别地, ;
; 中,
中, ,
, ,
, ,
, ,
, ,则
,则 ( )
( )  B .
B .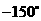 C.
C. D.
D.
 中,已知
中,已知 ,
, ,
, cm,解三角形;
cm,解三角形;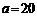 cm,
cm, cm,
cm, ,解三角形(角度精确到
,解三角形(角度精确到 ,边长精确到1cm)。
,边长精确到1cm)。

 ;
; ;
;

 <
<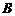 <
< ,所以
,所以 ,或
,或
 ,
,
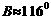 时,
时, ,
,

 ABC中,已知
ABC中,已知 ,
, ,
, ,求b及A;
,求b及A; ,
, ,
, ,解三角形
,解三角形
 cos
cos



 可以利用余弦定理,也可以利用正弦定理:
可以利用余弦定理,也可以利用正弦定理: ∴
∴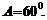
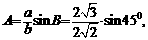
 >
>
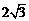 <
< ∴
∴ <
< ,即
,即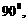
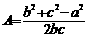


 ;
;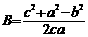
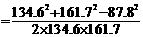
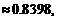
 ;
;

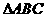 中,
中, ,
, ,
, ,求
,求 的值和
的值和
 ,
, 
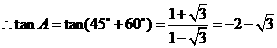 ,
,
 。
。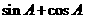 计算它的对偶关系式
计算它的对偶关系式 ①
①
 ,
,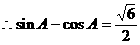 ②
② 。
。 。
。 。
。 中,
中, 则
则 的值等于 ,
的值等于 , 的取值范围为 .
的取值范围为 . 

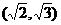
 由正弦定理得
由正弦定理得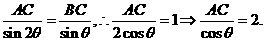
 ,
, ,故
,故 ,
,
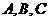 所对的边分别为
所对的边分别为 ,且满足
,且满足 ,
, .
. 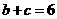 ,求
,求 的值.
的值. ,又由
,又由
 ,
,
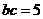 ,又
,又 或
或 ,由余弦定理得
,由余弦定理得 ,
,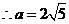
 、
、 ,已知
,已知 ,且
,且 求b
求b 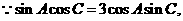 则由正弦定理及余弦定理有:
则由正弦定理及余弦定理有: 化简并整理得:
化简并整理得: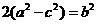 .又由已知
.又由已知 .解得
.解得 .
.  .又
.又 .
. ①
① ,
,
 ,即
,即
 ,故
,故 ②
② .
. ,求当A为何值时,
,求当A为何值时, 取得最大值,并求出这个最大值。
取得最大值,并求出这个最大值。 ,求
,求
 ,
, ,而
,而 ,所以
,所以 ,所以
,所以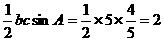
 ,所以
,所以

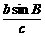 的值。
的值。 =a,再用正弦定理可求
=a,再用正弦定理可求 =
= =
= ,∴∠A=60°。
,∴∠A=60°。 ,∵b2=ac,∠A=60°,
,∵b2=ac,∠A=60°, =sin60°=
=sin60°= 。
。 的值。
的值。 =60°,故tan
=60°,故tan .由两角和的正切公式,
.由两角和的正切公式, 。
。
 。
。 为锐角,角
为锐角,角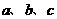 ,且
,且
 的值;
的值; ,求
,求



 ,∴
,∴ 
 得
得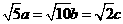 ,即
,即
 ∴
∴


 题型7:正余弦定理的实际应用
题型7:正余弦定理的实际应用 ,
, ,于水面C处测得B点和D点的仰角均为
,于水面C处测得B点和D点的仰角均为 ,AC=0.1km。试探究图中B,D间距离与另外哪两点间距离相等,然后求B,D的距离(计算结果精确到0.01km,
,AC=0.1km。试探究图中B,D间距离与另外哪两点间距离相等,然后求B,D的距离(计算结果精确到0.01km,
 1.414,
1.414,





 ;B点到M,
;B点到M, ;A,B的距离 d (如图所示) .
;A,B的距离 d (如图所示) .
 ;
;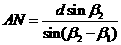 ;
; .
. ,
, ;B点到M,N点的府角
;B点到M,N点的府角 ,
, ;A,B的距离 d (如图所示).
;A,B的距离 d (如图所示). ;
; ;
; 
 ,这些解题思维的拐点,你能否很快的想到呢?
,这些解题思维的拐点,你能否很快的想到呢? ;
;
 (R为外接圆半径);
(R为外接圆半径); ,
, 。
。 aha=
aha= =
= =
= ;
;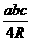 ;
; ;
; ;
;