0 445346 445354 445360 445364 445370 445372 445376 445382 445384 445390 445396 445400 445402 445406 445412 445414 445420 445424 445426 445430 445432 445436 445438 445440 445441 445442 445444 445445 445446 445448 445450 445454 445456 445460 445462 445466 445472 445474 445480 445484 445486 445490 445496 445502 445504 445510 445514 445516 445522 445526 445532 445540 447348
 的最大值和最小正周期分别为 ( )
的最大值和最小正周期分别为 ( ) ,2π D.
,2π D. ,π
,π 服从正态分布N(0,1),若P(
服从正态分布N(0,1),若P( 的值为( )
的值为( )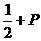 B.
B. C.
C. D.
D.
 ,
, 满足约束条件
满足约束条件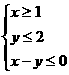 则
则 的取值范围是 ( )
的取值范围是 ( ) 在复平面内对应的点位于 ( )
在复平面内对应的点位于 ( ) 与(
与(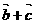 )都是非零向量,则
)都是非零向量,则 ,是
,是 则下列结论正确的是 ( )
则下列结论正确的是 ( ) B.
B.
 D.
D. 
 。
。 +
+ =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,过右焦点F且斜率为1的直线交椭圆C于A,B两点,N为弦AB的中点。
,过右焦点F且斜率为1的直线交椭圆C于A,B两点,N为弦AB的中点。 (
( =cos
=cos +sin
+sin 成立。
成立。 }的前项和为Sn,q为非零常数。已知对任意正整数n, m,当n > m时,
}的前项和为Sn,q为非零常数。已知对任意正整数n, m,当n > m时, 总成立。
总成立。 +
+ ≥
≥ 。
。 2)若二面角A -A1D - C的平面角为600,求
2)若二面角A -A1D - C的平面角为600,求 的值。
的值。