摘要:如图.正方形ABCD中.AB=6.点E在边CD上.且CD=3DE.将△ADE沿AE对折至△AFE.延长EF交边BC于点G.连接AG.CF.下列结论:①△ABG≌△AFG,②BG=GC,③AG∥CF,④S△FGC=3.其中正确结论的个数是( ) A.1 B.2 C.3 D.4 考点:翻折变换,全等三角形的判定与性质,勾股定理. 专题:几何综合题. 分析:根据翻折变换的性质和正方形的性质可证△ABG≌△AFG,在直角△ECG中.根据勾股定理可证BG=GC,通过证明∠AGB=∠AGF=∠GFC=∠GCF.由平行线的判定可得AG∥CF,由于S△FGC=S△GCE﹣S△FEC.求得面积比较即可. 解答:解:①正确.因为AB=AD=AF.AG=AG.∠B=∠AFG=90°.∴△ABG≌△AFG, ②正确.因为:EF=DE=CD=2.设BG=FG=x.则CG=6﹣x.在直角△ECG中.根据勾股定理.得2+42=(x+2)2.解得x=3.所以BG=3=6﹣3=GC, ③正确.因为CG=BG=GF.所以△FGC是等腰三角形.∠GFC=∠GCF.又∠AGB=∠AGF.∠AGB+∠AGF=180°﹣∠FGC=∠GFC+∠GCF. ∴∠AGB=∠AGF=∠GFC=∠GCF.∴AG∥CF, ④错误. 过F作FH⊥DC. ∵BC⊥DH. ∴FH∥GC. ∴△EFH∽△EGC. ∴=. EF=DE=2.GF=3. ∴EG=5. ∴==. ∴S△FGC=S△GCE﹣S△FEC=×3×4﹣×4×(×3)=≠3. 故选C. 点评:本题综合性较强.考查了翻折变换的性质和正方形的性质.全等三角形的判定与性质.勾股定理.平行线的判定.三角形的面积计算.有一定的难度.
网址:http://m.1010jiajiao.com/timu3_id_435733[举报]
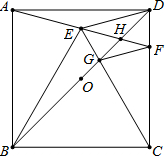 如图,正方形ABCD中,O为BD中点,以BC为边向正方形内作等边△BCE,连接并延长AE交CD于F,连接BD分别交 CE、AF于G、H,
如图,正方形ABCD中,O为BD中点,以BC为边向正方形内作等边△BCE,连接并延长AE交CD于F,连接BD分别交 CE、AF于G、H, 如图,正方形ABCD中,E是AD的中点,点F在DC上,且DC=4DF,试判断△BEF的形状,并证明你的结论.
如图,正方形ABCD中,E是AD的中点,点F在DC上,且DC=4DF,试判断△BEF的形状,并证明你的结论.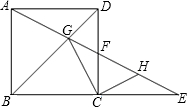 为EF的中点.
为EF的中点.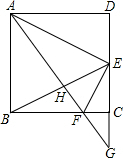 如图,正方形ABCD中,E为CD的中点,F为BC边上一点,且EF⊥AE,AF的延长线与DC的延长线交于点G,连接BE,与AF交于点H,则下列结论中不正确的是( )
如图,正方形ABCD中,E为CD的中点,F为BC边上一点,且EF⊥AE,AF的延长线与DC的延长线交于点G,连接BE,与AF交于点H,则下列结论中不正确的是( )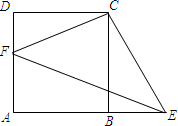 如图,正方形ABCD中,点F在AD上,点E在AB的延长线上,∠FCE=90°
如图,正方形ABCD中,点F在AD上,点E在AB的延长线上,∠FCE=90°