吉林省长春市2009年高中毕业班第一次调研考试
数 学 试 题(理)

注意事项:
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,试卷满分150分,考试时间120分。

第Ⅰ卷 (选择题,共60分)

一、选择题(本大题共12小题,每小题5分,共60分,在每小题的四个选项中,只有一项
是符合题目要求的,请将正确选项填在题后括号内)
1.已知集合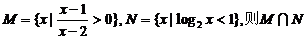 ( )
( )
A.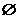 B.(0,1) C.(1,2) D.(-∞,1)
B.(0,1) C.(1,2) D.(-∞,1)
2.函数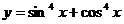 的最小正周期为 ( )
的最小正周期为 ( )
A.2π B.π C.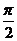 D.
D.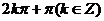

3.使不等式a>b成立的充要条件是 ( )
A.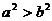 B.
B.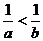 C.lga>lgb D.
C.lga>lgb D.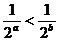

4.关于线、面的四个命题中不正确的是 ( )
A.平行于同一平面的两个平面一定平行
B.平行于同一直线的两条直线一定平行
C.垂直于同一直线的两条直线一定平行
D.垂直于同一平面的两条直线一定平行
5.已知椭圆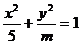 的离心率
的离心率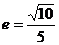 ,则m的值为 ( )
,则m的值为 ( )
A.3 B.3或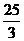 C.
C.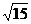 D.
D.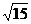 或
或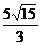

6.数列{an}是公差不为0的等差数列,且a6、a9、a15依次为等比数列{bn}的连续三项,若数 列{bn}的首项b1=
列{bn}的首项b1=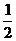 ,则数列{bn}的前5项和S5等于 ( )
,则数列{bn}的前5项和S5等于 ( )
A.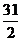 B.
B.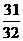 C.31 D.32
C.31 D.32
|
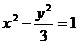 上一动点,F为双曲线的右焦点
上一动点,F为双曲线的右焦点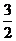 B.
B.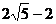 D.
D.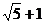

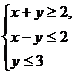 ,则
,则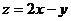 的最大值为
。
的最大值为
。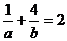 ,则
,则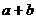 的最小值为
。
的最小值为
。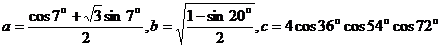 ,则a、b、
,则a、b、
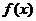 的单调增区间;
的单调增区间;
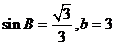 ,求△ABC的面积。
,求△ABC的面积。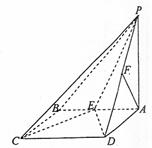 E、F分别为棱AB、PD的中点。
E、F分别为棱AB、PD的中点。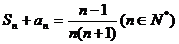 ,设
,设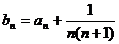
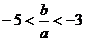 ;
;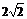 ≤| x1- x2|<3
≤| x1- x2|<3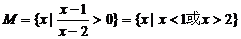 ,
,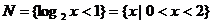 ,
,
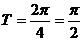 ,故选C。
,故选C。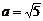 ,
,
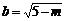 ,
,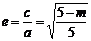
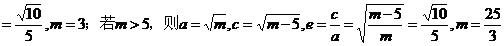 ,故
,故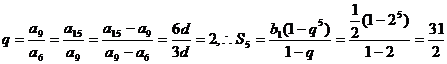 ,故选A。
,故选A。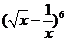 的展开式中常数项为第3项,
的展开式中常数项为第3项,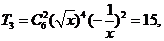 故选A。
故选A。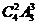 =36,故选D。
=36,故选D。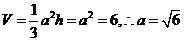 ,可利用三角形相似计算出r=2,S球=4πr2=16π,故
,可利用三角形相似计算出r=2,S球=4πr2=16π,故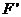 由双曲线定义可知,
由双曲线定义可知,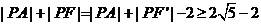 ,
,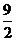 16.
16.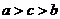
 简答与提示:
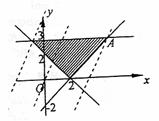
简答与提示: 按向量b=(-1,2)平移后得直线方程为
按向量b=(-1,2)平移后得直线方程为 :k:y=k(x-2)+b-1再将
:k:y=k(x-2)+b-1再将
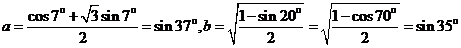
 cos54
cos54
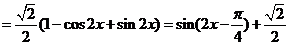 (4分)
(4分)
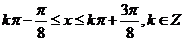 时,函数
时,函数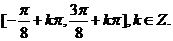 (6分)
(6分)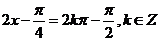 ,即
,即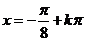 ,
, 时
时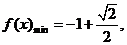
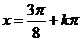 ,
,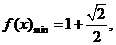 (10分)
(10分)

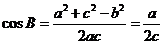 ,
,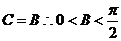 ,
,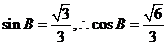 ,
,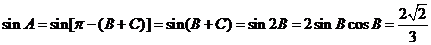 ,
, 。 (12分)
。 (12分)
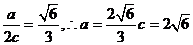
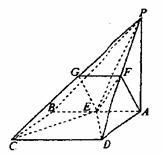 19.本小题主要考查空间线面关系,空间想象能力和推理运算能力或空间向量的应用。
19.本小题主要考查空间线面关系,空间想象能力和推理运算能力或空间向量的应用。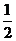 CD且FG∥CD,
CD且FG∥CD,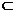 平面PCE,AF
平面PCE,AF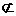 平面PCE, (4分)
平面PCE, (4分)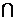 AD=A,
AD=A,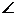 PDA=45°,
PDA=45°, ,GF=1,
,GF=1,

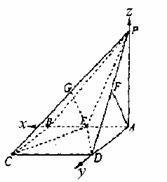 (1)由于PA⊥底面ABCD,且底面四边形ABCD是正方形,以A为坐标原点建立空间
(1)由于PA⊥底面ABCD,且底面四边形ABCD是正方形,以A为坐标原点建立空间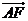 (0,1,1),
(0,1,1),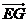 =(0,1,1),
=(0,1,1),




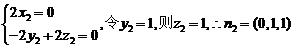 (6分)
(6分)
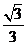 。 (8分)
。 (8分)

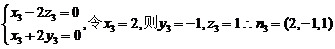 (10分)
(10分)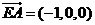 ,∴点A到平面PCE的距离
,∴点A到平面PCE的距离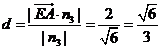 (12分)
(12分)

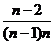 , (2分)
, (2分)

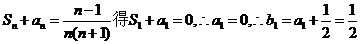 ,
,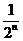 ,
,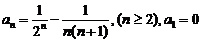 也合适
也合适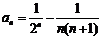 ,
,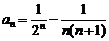 。(n∈N*)
。(n∈N*)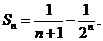 (8分)
(8分)
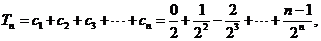
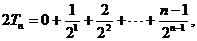
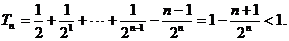 (12分)
(12分)
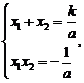 ∴
∴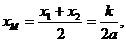

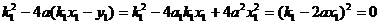
 =-1
=-1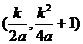 由(2)知道点N坐标为
由(2)知道点N坐标为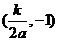 ,
,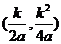 ,满足曲线C的方程,
,满足曲线C的方程,
 (5分)
(5分)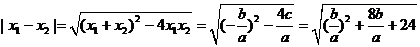
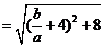
 (12分)
(12分)