摘要:5.考虑0<m<5或m>5两种情况.若0<m<5.则. .
网址:http://m.1010jiajiao.com/timu_id_273762[举报]
(2012•赣州模拟)某中学对某班50名学生学习习惯和数学学习成绩进行长期的调查,学习习惯和数学成绩都只分良好和一般两种情况,得到的统计数据(因某种原因造成数据缺省,现将缺省部分数据用x,y,z,m,n表示)如下表所示:
(1)在该班任选一名学习习惯良好的学生,求其数学成绩也良好的概率.
(2)已知A是学习习惯良好但数学成绩一般的学生,B是学习习惯一般但数学成绩良好的学生,在学习习惯良好但数学成绩一般的学生和学习习惯一般但数学成绩良好的学生中,各选取一学生作代表,求A、B至少有一个被选中的概率.
(3)有多大的把握认为该班的学生的学习习惯与数学成绩有关系?说明理由.
参考公式:Χ2=
;
临界值表:
查看习题详情和答案>>
| 数学成绩良好 | 数学成绩一般 | 合计 | |
| 学习习惯良好 | 20 | x | 25 |
| 学习习惯一般 | y | 21 | z |
| 合计 | 24 | m | n |
(2)已知A是学习习惯良好但数学成绩一般的学生,B是学习习惯一般但数学成绩良好的学生,在学习习惯良好但数学成绩一般的学生和学习习惯一般但数学成绩良好的学生中,各选取一学生作代表,求A、B至少有一个被选中的概率.
(3)有多大的把握认为该班的学生的学习习惯与数学成绩有关系?说明理由.
参考公式:Χ2=
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
临界值表:
| p(Χ2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
某中学对某班50名学生学习习惯和数学学习成绩进行长期的调查,学习习惯和数学成绩都只分良好和一般两种情况,得到的统计数据(因某种原因造成数据缺省,现将缺省部分数据用x,y,z,m,n表示)如下表所示:
(1)在该班任选一名学习习惯良好的学生,求其数学成绩也良好的概率.
(2)已知A是学习习惯良好但数学成绩一般的学生,B是学习习惯一般但数学成绩良好的学生,在学习习惯良好但数学成绩一般的学生和学习习惯一般但数学成绩良好的学生中,各选取一学生作代表,求A、B至少有一个被选中的概率.
(3)有多大的把握认为该班的学生的学习习惯与数学成绩有关系?说明理由.
参考公式: ;
;
临界值表:
查看习题详情和答案>>
| 数学成绩良好 | 数学成绩一般 | 合计 | |
| 学习习惯良好 | 20 | x | 25 |
| 学习习惯一般 | y | 21 | z |
| 合计 | 24 | m | n |
(2)已知A是学习习惯良好但数学成绩一般的学生,B是学习习惯一般但数学成绩良好的学生,在学习习惯良好但数学成绩一般的学生和学习习惯一般但数学成绩良好的学生中,各选取一学生作代表,求A、B至少有一个被选中的概率.
(3)有多大的把握认为该班的学生的学习习惯与数学成绩有关系?说明理由.
参考公式:
 ;
;临界值表:
| p(Χ2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看习题详情和答案>>
某中学对某班50名学生学习习惯和数学学习成绩进行长期的调查,学习习惯和数学成绩都只分良好和一般两种情况,得到的统计数据(因某种原因造成数据缺省,现将缺省部分数据用x,y,z,m,n表示)如下表所示:
| 数学成绩良好 | 数学成绩一般 | 合计 | |
| 学习习惯良好 | 20 | x | 25 |
| 学习习惯一般 | y | 21 | z |
| 合计 | 24 | m | n |
(2)已知A是学习习惯良好但数学成绩一般的学生,B是学习习惯一般但数学成绩良好的学生,在学习习惯良好但数学成绩一般的学生和学习习惯一般但数学成绩良好的学生中,各选取一学生作代表,求A、B至少有一个被选中的概率.
(3)有多大的把握认为该班的学生的学习习惯与数学成绩有关系?说明理由.
参考公式:
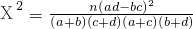 ;
;临界值表:
| p(Χ2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
已知函数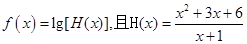 ,
,
(1)求函数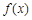 的定义域;
的定义域;
(2)求函数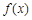 在区间
在区间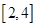 上的最小值;
上的最小值;
(3)已知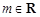 ,命题p:关于x的不等式
,命题p:关于x的不等式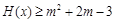 对函数
对函数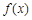 的定义域上的任意
的定义域上的任意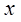 恒成立;命题q:指数函数
恒成立;命题q:指数函数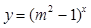 是增函数.若“p或q”为真,“p且q”为假,求实数m的取值范围.
是增函数.若“p或q”为真,“p且q”为假,求实数m的取值范围.
【解析】第一问中,利用由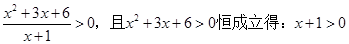 即
即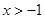
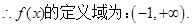
第二问中,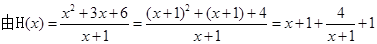 ,
,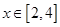 得:
得:
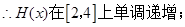
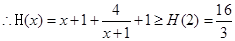 ,
,
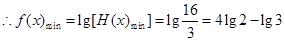
第三问中,由在函数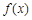 的定义域上
的任意
的定义域上
的任意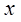 ,
,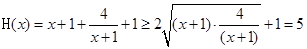 ,当且仅当
,当且仅当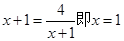 时等号成立。当命题p为真时,
时等号成立。当命题p为真时,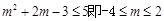 ;而命题q为真时:指数函数
;而命题q为真时:指数函数 .因为“p或q”为真,“p且q”为假,所以
.因为“p或q”为真,“p且q”为假,所以
当命题p为真,命题q为假时;当命题p为假,命题q为真时分为两种情况讨论即可 。
解:(1)由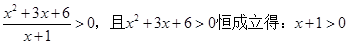 即
即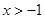
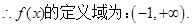
(2)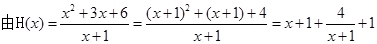 ,
,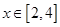 得:
得:
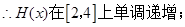
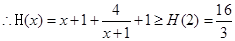 ,
,
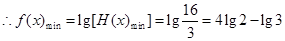
(3)由在函数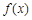 的定义域上
的任意
的定义域上
的任意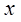 ,
,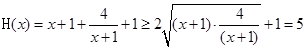 ,当且仅当
,当且仅当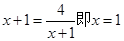 时等号成立。当命题p为真时,
时等号成立。当命题p为真时,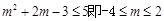 ;而命题q为真时:指数函数
;而命题q为真时:指数函数 .因为“p或q”为真,“p且q”为假,所以
.因为“p或q”为真,“p且q”为假,所以
当命题p为真,命题q为假时,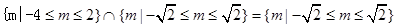
当命题p为假,命题q为真时,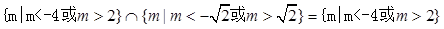 ,
,
所以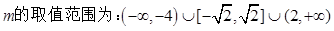
查看习题详情和答案>>