摘要：简答与提示:
网址：http://m.1010jiajiao.com/timu_id_273772[举报]
已知函数f(x)=
(ax-a-x)，a＞1．
（1）用a表示f（2），f（3），并化简；
（2）比较
与
，
与
的大小，并由此归纳出一个更一般的结论．（不要求写出证明过程）．
查看习题详情和答案>>
| a |
| a2-1 |
（1）用a表示f（2），f（3），并化简；
（2）比较
| f(2) |
| 2 |
| f(1) |
| 1 |
| f(3) |
| 3 |
| f(2) |
| 2 |
（2012•福建模拟）阅读下面材料：
根据两角和与差的正弦公式，有sin（α+β）=sinαcosβ+cosαsinβ------①
sin（α-β）=sinαcosβ-cosαsinβ------②
由①+②得sin（α+β）+sin（α-β）=2sinαcosβ------③
令α+β=A，α-β=B有α=
，β=
代入③得 sinA+sinB=2sin
cos
．
（Ⅰ）类比上述推证方法，根据两角和与差的余弦公式，证明：cosA-cosB=-2sin
sin
；
（Ⅱ）若△ABC的三个内角A，B，C满足cos2A-cos2B=2sin2C，试判断△ABC的形状．
（提示：如果需要，也可以直接利用阅读材料及（Ⅰ）中的结论）
查看习题详情和答案>>
根据两角和与差的正弦公式，有sin（α+β）=sinαcosβ+cosαsinβ------①
sin（α-β）=sinαcosβ-cosαsinβ------②
由①+②得sin（α+β）+sin（α-β）=2sinαcosβ------③
令α+β=A，α-β=B有α=
| A+B |
| 2 |
| A-B |
| 2 |
代入③得 sinA+sinB=2sin
| A+B |
| 2 |
| A-B |
| 2 |
（Ⅰ）类比上述推证方法，根据两角和与差的余弦公式，证明：cosA-cosB=-2sin
| A+B |
| 2 |
| A-B |
| 2 |
（Ⅱ）若△ABC的三个内角A，B，C满足cos2A-cos2B=2sin2C，试判断△ABC的形状．
（提示：如果需要，也可以直接利用阅读材料及（Ⅰ）中的结论）
如图，平面EAD⊥平面ABCD，△ADE是等边三角形，ABCD是矩形，F是AB的中点，G是AD的中点，EC与平面ABCD成30°角，（1）（理、文）求证EG⊥平面ABCD；
（2）（理、文）当AD的长是多少时，D点到平面EFC的距离为2？请说明理由．
（3）（理答文不答）若AD=2，求二面角E-FC-G的度数．
选做题（这里给出了3道选做题，考生只能从中选做一题，多答时按顺序只评第1位置题）A．在极坐标中，圆ρ=2cosθ的圆心的极坐标是
| π |
| 4 |
是
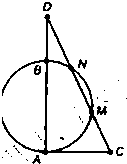
B．如图，AB为⊙O的直径，AC切⊙O于点A，且AC=2
| 2 |
C．若关于x的不等式|x-2|+|x-3|＜a的解集为∅，则α实数的取值范围是
阅读下面材料：
根据两角和与差的正弦公式，有：
sin（α+β）=sinαcosβ+cosαsinβ…①
sin（α-β）=sinαcosβ-cosαsinβ…②
由①+②得sin（α+β）+sin（α-β）=2sinαcosβ…③
令α+β=A，α-β=B有α=
，β=
代入③得sinA+sinB=2sin
cos
．
（Ⅰ）类比上述推理方法，根据两角和与差的余弦公式，证明：cosA-cosB=-2sin
sin
；
（Ⅱ）若△ABC的三个内角A，B，C满足cos2A-cos2B=1-cos2C，试判断△ABC的形状．（提示：如果需要，也可以直接利用阅读材料及（Ⅰ）中的结论）
查看习题详情和答案>>
根据两角和与差的正弦公式，有：
sin（α+β）=sinαcosβ+cosαsinβ…①
sin（α-β）=sinαcosβ-cosαsinβ…②
由①+②得sin（α+β）+sin（α-β）=2sinαcosβ…③
令α+β=A，α-β=B有α=
| A+B |
| 2 |
| A-B |
| 2 |
代入③得sinA+sinB=2sin
| A+B |
| 2 |
| A-B |
| 2 |
（Ⅰ）类比上述推理方法，根据两角和与差的余弦公式，证明：cosA-cosB=-2sin
| A+B |
| 2 |
| A-B |
| 2 |
（Ⅱ）若△ABC的三个内角A，B，C满足cos2A-cos2B=1-cos2C，试判断△ABC的形状．（提示：如果需要，也可以直接利用阅读材料及（Ⅰ）中的结论）