摘要:△= ∴k1=2ax1.(也可利用导数直接得出此结论). ∴直线l1方程可化为y=2ax1x-ax12 ① 同理.以Q为切点的切线l2方程可化为y=2ax2x-ax22 ②.
网址:http://m.1010jiajiao.com/timu_id_273850[举报]
(本小题满分12分)
已知函数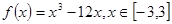 ;
;
(1)求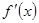 ; (2)求
; (2)求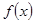 的最大值与最小值.
的最大值与最小值.
【解析】第一问利用导数的运算法则,幂函数的导数公式,可得。
第二问中,利用第一问的导数,令导数为零,得到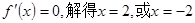
然后结合导数,函数的关系判定函数的单调性,求解最值即可。
查看习题详情和答案>>
已知四棱锥P-ABCD的底面ABCD是边长为2的正方形,PD⊥底面ABCD,E,F分别为棱BC、AD的中点.
(1)求证:DE∥平面PFB;
(2)已知二面角P-BF-C的余弦值为 ,求四棱锥P-ABCD的体积.
,求四棱锥P-ABCD的体积.

【解析】(1)证:DE//BF即可;
(2)可以利用向量法根据二面角P-BF-C的余弦值为 ,确定高PD的值,即可求出四棱锥的体积.也可利用传统方法直接作出二面角的平面角,求高PD的值也可.在找平面角时,要考虑运用三垂线或逆定理.
,确定高PD的值,即可求出四棱锥的体积.也可利用传统方法直接作出二面角的平面角,求高PD的值也可.在找平面角时,要考虑运用三垂线或逆定理.
查看习题详情和答案>>
已知函数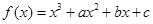 ,曲线
,曲线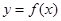 在点
在点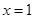 处的切线为
处的切线为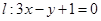 ,若
,若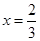 时,
时,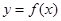 有极值.
有极值.
(1)求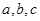 的值;
的值;
(2)求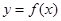 在
在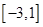 上的最大值和最小值.
上的最大值和最小值.
【解析】(1)根据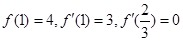 可建立关于a,b,c的三个方程,解方程组即可.
可建立关于a,b,c的三个方程,解方程组即可.
(2)在(1)的基础上,利用导数列表求极值,最值即可.
查看习题详情和答案>>
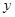 (单位:千克)与销售价格
(单位:千克)与销售价格 (单位:元/千克)满足关系式
(单位:元/千克)满足关系式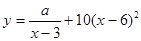 ,其中
,其中 ,
, 为常数,已知销售价格为5元/千克时,每日可售出该商品11千克.
为常数,已知销售价格为5元/千克时,每日可售出该商品11千克. (销售单价-成品单价),然后利用导数求其最值即可.
(销售单价-成品单价),然后利用导数求其最值即可. 在
在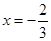 与
与 时都取得极值.
时都取得极值. 的值及函数
的值及函数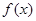 的单调区间;www.7caiedu.cn
的单调区间;www.7caiedu.cn  ,不等式
,不等式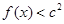 恒成立,求
恒成立,求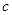 的取值范围.
的取值范围. 的两个根,可求出a,b的值,然后利用导数确定其单调区间即可.
的两个根,可求出a,b的值,然后利用导数确定其单调区间即可. ,即可解出c的取值范围.
,即可解出c的取值范围.