摘要：已知数列{an}满足关系式.设
网址：http://m.1010jiajiao.com/timu_id_273747[举报]
已知数列{an}满足a1=7，an+1=3an+2n-1-8n．（n∈N*）
（Ⅰ）李四同学欲求{an}的通项公式，他想，如能找到一个函数f（n）=A•2n-1+B•n+C（A、B、C是常数），把递推关系变成an+1-f（n+1）=3[an-f（n）]后，就容易求出{an}的通项了．请问：他设想的f（n）存在吗？{an}的通项公式是什么？
（Ⅱ）记Sn=a1+a2+a3+…+an，若不等式Sn-2n2＞p×3n对任意n∈N*都成立，求实数p的取值范围． 查看习题详情和答案>>
（Ⅰ）李四同学欲求{an}的通项公式，他想，如能找到一个函数f（n）=A•2n-1+B•n+C（A、B、C是常数），把递推关系变成an+1-f（n+1）=3[an-f（n）]后，就容易求出{an}的通项了．请问：他设想的f（n）存在吗？{an}的通项公式是什么？
（Ⅱ）记Sn=a1+a2+a3+…+an，若不等式Sn-2n2＞p×3n对任意n∈N*都成立，求实数p的取值范围． 查看习题详情和答案>>
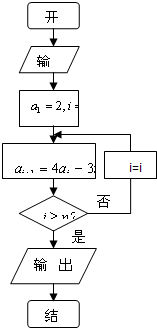已知数列{an}满足如图所示的程序框图．（I）写出数列{an}的一个递推关系式；并求数列{an}的通项公式
（Ⅱ）设数列{an}的前n项和Sn，证明不等式Sn+1≤4Sn，对任意n∈N*皆成立．
已知数列{an}满足a1=7，an+1=3an+2n-1-8n（n∈N*）。
（1）李四同学欲求{an}的通项公式，他想，如能找到一个函数f（n）=A·2n-1+B·n+C（A、B、C是常数），把递推关系变成an+1-f（n+1）=3[an-f（n）]后，就容易求出{an}的通项了。请问：他设想的f（n）存在吗？{an}的通项公式是什么？
（2）记Sn=a1+a2+a3+…+an，若不等式Sn-2n2>p×3n 对任意n∈N*都成立，求实数p的取值范围。