极坐标高考题的几种常见题型
一、极坐标方程与直角坐标方程的互化
互化公式: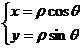 或
或 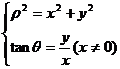
θ的象限由点(x,y)所在的象限确定.
例1(2007海南宁夏)⊙O1和⊙O2的极坐标方程分别为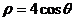 ,
,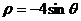 .
.
(I)把⊙O1和⊙O2的极坐标方程化为直角坐标方程;
(II)求经过⊙O1,⊙O2交点的直线的直角坐标方程.
解:以极点为原点,极轴为x轴正半轴,建立平面直角坐标系,两坐标系中取相同的长度单位.
(I)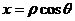 ,
,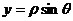 ,由
,由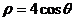 得
得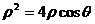 .所以
.所以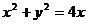 .
.
即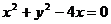 为⊙O1的直角坐标方程.
为⊙O1的直角坐标方程.
同理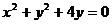 为⊙O2的直角坐标方程.
为⊙O2的直角坐标方程.
(II)解法一:由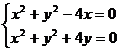 解得
解得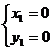 ,
,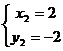
即⊙O1,⊙O2交于点(0,0)和(2,-2).过交点的直线的直角坐标方程为y=-x.
解法二: 由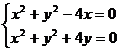 ,两式相减得-4x-4y=0,即过交点的直线的直角坐标方程为y=-x.
,两式相减得-4x-4y=0,即过交点的直线的直角坐标方程为y=-x.
评述:本题主要考查曲线的极坐标方程化为直角坐标方程的方法及两圆公共弦所在直线方程的求法.
例2(2003全国)圆锥曲线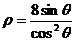 的准线方程是
的准线方程是
(A)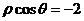 (B)
(B)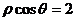 (C)
(C) 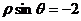 (D)
(D) 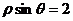
解: 由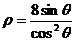 去分母后两边同时乘以
去分母后两边同时乘以 得:
得: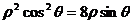 ,所以x2=8y ,其准线方程为y=
,所以x2=8y ,其准线方程为y=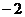 ,在极坐标系中方程为
,在极坐标系中方程为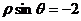 ,故选C.
,故选C.
例3(1998年上海)以直角坐标系的原点O为极点,x轴的正半轴为极轴
建立极坐标系,若椭圆两焦点的极坐标分别是(1,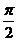 ),(1,
),(1,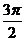 ),长轴长是4,则此 椭圆的直角坐标方程是_______________.
),长轴长是4,则此 椭圆的直角坐标方程是_______________.
解:由已知条件知椭圆两焦点的直角坐标为(0,1),(0,-1).c=1,a=2,b2=a2-c2=3,
故所求椭圆的直角坐标方程为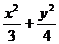 =1
=1
评述:点的直角坐标与极坐标的互化、曲线的极坐标方程与直角坐标方程的 互化要熟练掌握.
类题:1(1995年上海)把直角坐标系的原点作为极点,x轴的正半轴作为极轴,并且在两种坐标系中取相同的长度单位.若曲线的极坐标方程是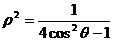 ,则它的直角坐标方程是___________.
(答案:3x2-y2=1)
,则它的直角坐标方程是___________.
(答案:3x2-y2=1)
2(1998年全国)曲线的极坐标方程 =4sin
=4sin 化成直角坐标方程为
化成直角坐标方程为
(A) x2+(y+2)2=4 (B) x2+(y-2)2=4
(C) (x-2)2+y2=4 (D) (x+2)2+y2=4 (答案:B)
3(2002北京)已知某曲线的参数方程是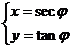 (
(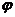 为参数)若以原点为极点,x轴的正半轴为极轴,长度单位不变,建立极坐标系,则该曲线的极坐标方程是
为参数)若以原点为极点,x轴的正半轴为极轴,长度单位不变,建立极坐标系,则该曲线的极坐标方程是
(A)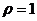 (B)
(B)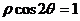 (C)
(C)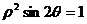 (D)
(D) 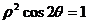 (答案:D)
(答案:D)
常见的直线和圆的极坐标方程及极坐标系中的旋转不变性:
二、已知曲线的极坐标方程,判断曲线类型
1、直线的极坐标方程(a>0)
(1)过极点,并且与极轴成α角的直线的极坐标方程: =α;
=α;
(2)垂直于极轴和极点间的距离为a的直线的极坐标方程: cos
cos =a;
=a;
(3)平行于极轴和极轴间的距离为a的直线的极坐标方程: sin
sin =a;
=a;
(4)不过极点,和极轴成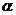 角,到极点距离为a的直线的极坐标方程:
角,到极点距离为a的直线的极坐标方程:
 sin(α-θ)=a.
sin(α-θ)=a.
2、圆的极坐标方程(a>0)
(1)圆心在极点,半径为a的圆的极坐标方程:  =a;
=a;
(2)圆心在(a,0),半径为a的圆的极坐标方程:  =2acos
=2acos ;
;
(3)圆心在(a,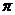 ),半径为a的圆的极坐标方程:
),半径为a的圆的极坐标方程:  =
=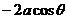 ;
;
(4)圆心在(a,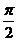 ),半径为a的圆的极坐标方程:
),半径为a的圆的极坐标方程:  =2asin
=2asin ;
;
(5)圆心在(a,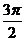 ),半径为a的圆的极坐标方程:
),半径为a的圆的极坐标方程:  =
=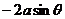 ;
;
(6)圆心在(a,  0),半径为a的圆的极坐标方程:
0),半径为a的圆的极坐标方程:  =2acos(
=2acos( -
- 0).
0).
3、极坐标系中的旋转不变性:
曲线f( ,
, +
+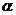 )=0是将曲线f(
)=0是将曲线f( ,
, )=0绕极点旋转|
)=0绕极点旋转|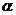 |角(
|角(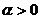 时,按顺
时,按顺
时针方向旋转,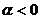 时,按逆时针方向旋转)而得到.
时,按逆时针方向旋转)而得到.
例4(1990年全国)极坐标方程4 sin2
sin2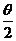 =5所表示的曲线是
=5所表示的曲线是
(A)圆 (B)椭圆 (C)双曲线的一支 (D)抛物线
解:由已知极坐标方程及三角公式得:2 (1-cos
(1-cos )=5,
)=5,
∴2 =2
=2 cos
cos +5,由互化公式得2
+5,由互化公式得2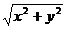 =2x+5,平方整理得
=2x+5,平方整理得
y2=5(x+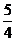 ),方程表示的曲线是抛物线,故选D.
),方程表示的曲线是抛物线,故选D.
评述:对于给出的极坐标方程相对于极坐标系而言不是标准的,一般将其等价转 化为直角坐标方程来判断其曲线类型.
类题:1(1991年三南)极坐标方程4sin2 =3表示的曲线是
=3表示的曲线是
(A)二条射线 (B)二条相交直线 (C) 圆 (D) 抛物线 (答案:B)
2(1987年全国)极坐标方程 =sin
=sin +2cos
+2cos 所表示的曲线是
所表示的曲线是
(A)直线 (B)圆 (C)双曲线 (D) 抛物线 (答案:B)
3(2001年广东、河南)极坐标方程 2cos2
2cos2 =1所表示的曲线是
=1所表示的曲线是
(A)两条相交直线 (B)圆 (C)椭圆 (D)双曲线 (答案:D)
4(2003北京)极坐标方程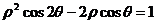 表示的曲线是
表示的曲线是
(A)圆 (B)椭圆 (C)抛物线 (D)双曲线 (答案:D)
例5(1994年全国)极坐标方程 =cos(
=cos(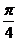 -
- )所表示的曲线是
)所表示的曲线是
(A) 双曲线 (B)椭圆 (C)抛物线 (D)圆
解:曲线 =cos(
=cos(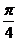 -
- )=cos(
)=cos( -
-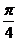 )是把圆
)是把圆 =cos
=cos 绕极点按逆时针方向旋
绕极点按逆时针方向旋
转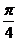 而得,曲线的形状仍然是一个圆,故选D
而得,曲线的形状仍然是一个圆,故选D
评述:把曲线的极坐标方程化为直角坐标方程较为麻烦,利用旋转不变性则更容易得出答案.方程 cos(
cos( -
- 0)=0表示一条直线,方程
0)=0表示一条直线,方程 =acos(
=acos( -
- 0)表示半径为
0)表示半径为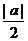 ,
,
圆心为(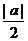 ,
, 0)的圆,要注意两者的区别.
0)的圆,要注意两者的区别.
 例6(2001年全国)极坐标方程
例6(2001年全国)极坐标方程 =2sin(
=2sin( +
+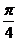 )的图形是
)的图形是
(A) (B) (C) (D)
解:圆 =2sin(
=2sin( +
+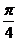 )是把圆
)是把圆 =2sin
=2sin 绕极点按顺时针方向旋转
绕极点按顺时针方向旋转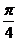 而得,圆心的极坐标为(1,
而得,圆心的极坐标为(1,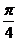 ),故选C.
),故选C.
类题:1(2002江苏)极坐标方程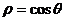 与
与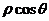 =
=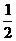 的图形是
的图形是
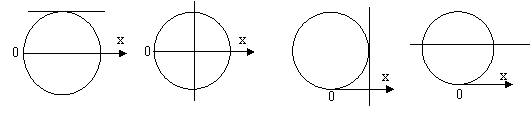
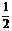
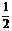
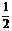
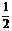
(A) (B) (C) (D)
(答案:B)
2(2004北京春)在极坐标系中,圆心在(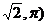 且过极点的圆的方程为
且过极点的圆的方程为
(A) 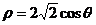 (B)
(B)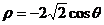 (C)
(C)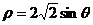 (D)
(D)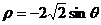
(答案:B)
三、判断曲线位置关系
例7(2000年京皖春)直线 =
=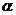 和直线
和直线 sin(
sin( -
-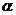 )=1的位置关系
)=1的位置关系
(A) 垂直 (B) 平行 (C) 相交但不垂直 (D) 重合
解:直线 sin(
sin( -
-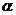 )=1是把直线
)=1是把直线 sin
sin =1绕极点按逆时针方向旋转
=1绕极点按逆时针方向旋转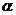 角
而得, 从而两直线平行,故选B.
角
而得, 从而两直线平行,故选B.
评注:对直线 sin(
sin( -
-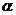 )=1与直线
)=1与直线 sin
sin =1的关系要十分熟悉.
=1的关系要十分熟悉.
例8(2002北京春)在极坐标系中,如果一个圆的方程是r=4cosq+6sinq,那么过圆心且与极轴平行的直线方程是
(A) rsinq=3 (B) rsinq = ?3 (C) rcosq =2 (D) rcosq = ?2
四、根据条件求直线和圆的极坐标方程
解:将圆的极坐标方程化为直角坐标方程得:x2+y2=4x+6y,即(x-2)2+(y-3)2=13.
圆心为(2,3),所求直线方程为y=3,即rsinq=3,故选A.
评述:注意直线的直角坐标方程极易求出.
类题:1(1992年上海)在极坐标方程中,与圆 =4sin
=4sin 相切的一条直线的方程是
相切的一条直线的方程是
(A)  sin
sin =2 (B)
=2 (B) cos
cos =2 (C)
=2 (C) cos
cos = 4 (D)
= 4 (D)  cos
cos =- 4(答案:B)
=- 4(答案:B)
2(1993年上海)在极坐标方程中,过点M(2,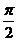 )且平行于极轴的直线的极坐标方程是_______.
(答案:
)且平行于极轴的直线的极坐标方程是_______.
(答案:  sin
sin =2)
=2)
3(1994年上海)已知点P的极坐标为(1,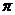 ),那么过点P且垂直于极轴的
),那么过点P且垂直于极轴的
直线的极坐标方程为
(A) =1
(B)
=1
(B) =cos
=cos (C)
(C) =
=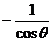 (D)
(D) =
=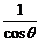 (答案:C)
(答案:C)
4(2000年全国)以极坐标系中点(1,1)为圆心,1为半径的圆的方程是
(A) =2cos(
=2cos( -
-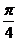 ) (B)
) (B) =2sin(
=2sin( -
-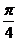 ) (C)
) (C) =2cos(
=2cos( -1) (D)
-1) (D) =2sin(
=2sin( -1)
-1)
(答案:C)
五、求曲线中点的极坐标
例9(2003上海)在极坐标系中,定点A(1,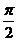 ),点B在直线
),点B在直线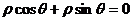 上运动,当线段AB最短时,点B的极坐标是_________.
上运动,当线段AB最短时,点B的极坐标是_________.
解:在直角坐标系中,A点坐标为(0,1),B在直线x+y=0上, AB最短,则B为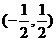 ,化为极坐标为
,化为极坐标为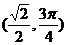 .
.
例10(1999年上海)极坐标方程5 2cos2
2cos2 +
+ 2-24=0所表示的曲线焦点的极坐标为__________.
2-24=0所表示的曲线焦点的极坐标为__________.
解:由5 2cos2
2cos2 +
+ 2-24=0得5
2-24=0得5 2(cos2
2(cos2 -sin2
-sin2 )+
)+ 2-24=0化为直角坐标方程得
2-24=0化为直角坐标方程得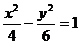 ,该双曲线的焦点的直角坐标为(
,该双曲线的焦点的直角坐标为(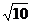 ,0)与(-
,0)与(-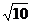 ,0),故所求 焦点的极坐标为(
,0),故所求 焦点的极坐标为(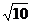 ,0)、(
,0)、(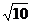 ,
,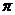 ).
).
评述:本题考查圆锥曲线极坐标方程的基础知识,掌握点的直角坐标与极坐标 的对应关系极为有用.
例11(2001年京皖蒙春)极坐标系中,圆 =4cos
=4cos +3sin
+3sin 的圆心的坐标是
的圆心的坐标是
(A) (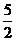 ,arcsin
,arcsin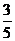 ) (B)(5,arcsin
) (B)(5,arcsin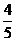 ) (C)(5,arcsin
) (C)(5,arcsin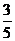 ) (D)(
) (D)(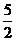 ,arcsin
,arcsin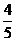 )
)
解:由 = 4cos
= 4cos +3sin
+3sin =5(
=5(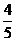 cos
cos +
+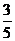 sin
sin )=5cos(
)=5cos( -φ)(其中sinφ=
-φ)(其中sinφ=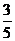 )
)
所以所求圆心坐标为(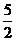 ,arcsin
,arcsin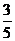 ),故选A.
),故选A.
类题:(2002上海)若A、B两点的极坐标为A(4,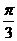 ),B(6,0),则AB中点的极坐标是_________.(极角用反三角函数值表示).
答案.(
),B(6,0),则AB中点的极坐标是_________.(极角用反三角函数值表示).
答案.(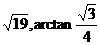 )
)
六、求距离
例12(2007广东文)在极坐标系中,直线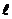 的方程为ρsinθ=3,则点(2,
的方程为ρsinθ=3,则点(2,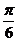 )到直线
)到直线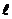 的距离为___________.
的距离为___________.
解: 将直线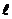 的极坐标方程ρsinθ=3化为直角坐标系方程得:y=3,
的极坐标方程ρsinθ=3化为直角坐标系方程得:y=3,
点(2,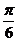 )在直角坐标系中为(
)在直角坐标系中为(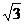 ,1),故点(2,
,1),故点(2,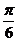 ) 到直线
) 到直线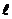 的距离为2.
的距离为2.
评注:本题主要考查极坐标系与直角坐标系之间的互化.
例13(1992年全国、1996年上海)极坐标方程分别是 =cos
=cos 和
和 =sin
=sin 的两个圆的圆心距是
的两个圆的圆心距是
(A) 2
(B) 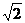 (C) 1
(D)
(C) 1
(D) 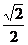
解法一:两圆的圆心坐标分别为(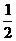 ,0)与(
,0)与(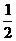 ,
,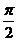 ),由此求得圆心距为
),由此求得圆心距为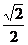 ,选D.
,选D.
解法二:将极坐标方程化成直角坐标方程得(x-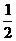 )2+y2=
)2+y2=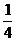 与x2+(y-
与x2+(y-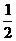 )2=
)2=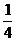 ,
,
由此求得圆心距为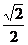 ,选D.
,选D.
评述:本题考查对极坐标的理解,理解深刻者可在极坐标系上画出简图直接求解,
一般理解者,化极坐标方程为直角坐标方程也能顺利得到正确答案.
例14(1997年全国)已知直线的极坐标方程为 sin(
sin( +
+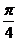 )=
)=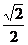 ,则极点到该直线的距离是_______.
,则极点到该直线的距离是_______.
解法一:化直线方程为 =
=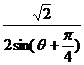 ,根据极坐标的概念极点到该直线
,根据极坐标的概念极点到该直线
的距离等于这个函数ρ的最小值,当sin( +
+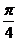 )=1时,
)=1时,  取最小值
取最小值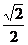 即为所求.
即为所求.
解法二:对极坐标欠熟悉时,可把直线的极坐标方程化为直角坐标方程x+y=1,
应用点到直线的距离公式得原点到此直线的距离为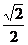 .
.
类题:1(2000年上海)在极坐标系中,若过点(3,0)且与极轴垂直的直线交曲线 = 4cos
= 4cos 于A、B两点,则|AB|=______.
(答案:2
于A、B两点,则|AB|=______.
(答案:2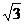 )
)
2(2004上海)在极坐标系中,点M(4,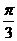 )到直线
)到直线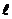 :
: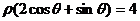 的距离d=__________________.
(答案:
的距离d=__________________.
(答案: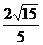 )
)
七、判定曲线的对称性
例15(1999年全国)在极坐标系中,曲线 = 4sin(
= 4sin( -
-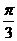 )关于
)关于
(A) 直线 =
=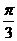 轴对称 (B)直线
轴对称 (B)直线 =
=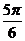 轴对称
轴对称
(C) 点(2, 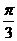 )中心对称 (D)极点中心对称
)中心对称 (D)极点中心对称
解:把圆 = 4sin
= 4sin 绕极点按逆时针方向旋转
绕极点按逆时针方向旋转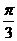 便得到曲线
便得到曲线
 = 4sin(
= 4sin( -
-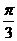 )=
)=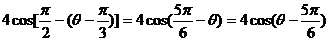 ,
,
知其圆心坐标为(2,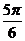 ),故圆的对称轴为
),故圆的对称轴为 =
=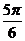 ,应选B.
,应选B.
评述:方程表示的曲线是圆,为弄清轴对称或中心对称的问题,关键是求出其
圆心的坐标.
八、求三角形面积
 例16(2006上海)在极坐标系中,O是极点,设点A(4,
例16(2006上海)在极坐标系中,O是极点,设点A(4,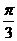 ),B(5,
),B(5,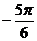 ),则△OAB的面积是 .
),则△OAB的面积是 .
解:如图所示,在△OAB中,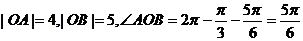
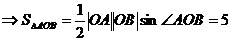
评述:本题考查极坐标及三角形面积公式.