摘要:(I)..由得.所以.
网址:http://m.1010jiajiao.com/timu_id_51893[举报]
解:因为有负根,所以![]() 在y轴左侧有交点,因此
在y轴左侧有交点,因此![]()
解:因为函数没有零点,所以方程![]() 无根,则函数y=x+|x-c|与y=2没有交点,由图可知c>2
无根,则函数y=x+|x-c|与y=2没有交点,由图可知c>2
13.证明:(1)令x=y=1,由已知可得f(1)=f(1×1)=f(1)f(1),所以f(1)=1或f(1)=0
若f(1)=0,f(0)=f(1×0)=f(1)f(0)=0,所以f(1)=f(0)与已知条件“![]() ”矛盾所以f(1)≠0,因此f(1)=1,所以f(1)-1=0,1是函数y=f(x)-1的零点
”矛盾所以f(1)≠0,因此f(1)=1,所以f(1)-1=0,1是函数y=f(x)-1的零点
(2)因为f(1)=f[(-1)×(-1)]=f2(-1)=,所以f(-1)=±1,但若f(-1)=1,则f(-1)=f(1)与已知矛盾所以f(-1)不能等于1,只能等于-1。所以任x∈R,f(-x)=f(-1)f(x)=-f(x),因此函数是奇函数
数字1,2,3,4恰好排成一排,如果数字i(i=1,2,3,4)恰好出现在第i个位置上则称有一个巧合,求巧合数![]() 的分布列。
的分布列。
用n个不同的实数a1,a2,…,an可得到n!个不同的排列,每个排列为一行写成一个n!行的数阵。对第i行 ,记
,记 ,i=1,2,3,…,n!。例如:用1,2,3可得数阵如图,由于此数阵中每一列各数之和都是12,所以,b1+b2+…+b6=-12+2×12-3×12=-24,那么,在用1,2,3,4,5形成的数阵中,b1+b2+…+b120=
,i=1,2,3,…,n!。例如:用1,2,3可得数阵如图,由于此数阵中每一列各数之和都是12,所以,b1+b2+…+b6=-12+2×12-3×12=-24,那么,在用1,2,3,4,5形成的数阵中,b1+b2+…+b120=
 ,记
,记 ,i=1,2,3,…,n!。例如:用1,2,3可得数阵如图,由于此数阵中每一列各数之和都是12,所以,b1+b2+…+b6=-12+2×12-3×12=-24,那么,在用1,2,3,4,5形成的数阵中,b1+b2+…+b120=
,i=1,2,3,…,n!。例如:用1,2,3可得数阵如图,由于此数阵中每一列各数之和都是12,所以,b1+b2+…+b6=-12+2×12-3×12=-24,那么,在用1,2,3,4,5形成的数阵中,b1+b2+…+b120=
[ ]
A.-3600
B.1800
C.-1080
D.-720
查看习题详情和答案>>
B.1800
C.-1080
D.-720
用n个不同的实数a1,a2,…an可得n!个不同的排列,每个排列为一行写成(1 2 3)
一个n!行的数阵.对第i行ai1,ai2,…ain,记bi=-ai1+2ai2-3ai3+…+(-1)nnain,(1 3 2)
i=1,2,3,…,n!.用1,2,3可你数阵如下,由于此数阵中每一列各数之和都(2 1 3)是12,所以,b1+b2+…+b6=-12+2×12-3×12=-24.那么,在用1,2,3,4,5形成(2 3 1)的数阵中,求b1+b2+…+b120的值.(3 1 2)(3 2 1)
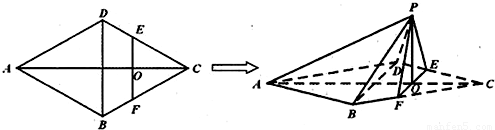
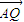 =λ
=λ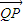 (λ>0),试探究:直线OQ与平面PBD所成角的大小是否一定大于
(λ>0),试探究:直线OQ与平面PBD所成角的大小是否一定大于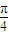 ?并说明理由.
?并说明理由.