




 二○○七年福州市初中毕业会考、高级中等学校招生考试
二○○七年福州市初中毕业会考、高级中等学校招生考试
数 学 试 卷 答 案
二、填空题:(共5小题,每题4分,满分20分.)
11. (x - 3)2 12. ≥ 3 13. ∠B = ∠C、 ∠AEB = ∠ADC、 ∠CEO = ∠BDO、
AB = AC、BD = CE (任选一个即可) 14. 8π 15. 76
三、解答题:(满分100分)
16.(每小题8分,满分16分)
(1)解:原式 = 6 ? 1 + 9 = 14
(2)解:原式 = 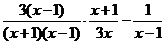 =
= 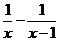 =
= 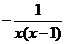
当  = 2 时,原式 =
= 2 时,原式 = 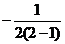 =
= 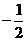
17.(每小题8分,满分16分)
(1) 以下为不同情形下的部分正确画法,答案不唯一. (满分8分)

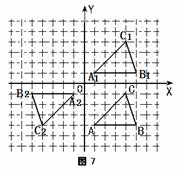 (2) 画图答案如图所示:
(2) 画图答案如图所示:
① C1 ( 4 ,4 ) ;
② C2 ( - 4 , - 4 ) (满分8分).
 18.(本题满分10分)
18.(本题满分10分)
(1)  = 12 ;
= 12 ;
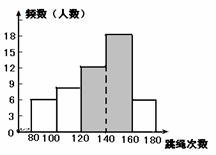
(2) 画图答案如图所示:
(3) 中位数落在第 3 组 ;
(4) 只要是合理建议.
19.(本题满分10分)
(1) 证明:如图8,连结
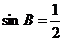
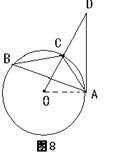 ∵ , ∴ ∠B = 30°.
∵ , ∴ ∠B = 30°.
∵ ∠AOC = 2 ∠B , ∴ ∠AOC = 60°.
∵ ∠D = 30°, ∴ ∠OAD = 180°- ∠D - ∠AOD = 90°.
∴ AD是⊙O的切线.
(2) 解:∵ OA = OC ,∠AOC = 60°,
∴ △AOC是等边三角形 . ∴ OA = AC = 6 .
∵ ∠OAD = 90°主题:,∠D = 30°, ∴ AD = 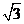 AO =
AO = 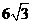 .
.
20. (本题满分10分)
解:①依题意,得 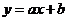 ,
, 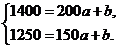
解得 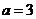 ,
,
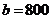 .
.
②依题意,得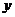 ≥ 1800, 即3
≥ 1800, 即3 + 800 ≥ 1800, 解得
+ 800 ≥ 1800, 解得 ≥
≥ 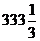 .
.
答:小俐当月至少要卖服装334件.
21. (本题满分12分)
(1)解法一:如图9-1
延长BP交直线AC于点E
∵ AC∥BD , ∴ ∠PEA = ∠PBD .
∵ ∠APB = ∠PAE + ∠PEA ,
∴ ∠APB = ∠PAC + ∠PBD .
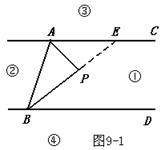
解法二:如图9-2
过点P作FP∥AC ,
∴ ∠PAC = ∠APF .
∵ AC∥BD , ∴FP∥BD .
 ∴ ∠FPB =∠PBD .
∴ ∠FPB =∠PBD .
∴ ∠APB =∠APF +∠FPB =∠PAC + ∠PBD .
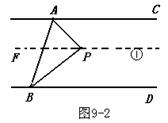
解法三:如图9-3,
∵ AC∥BD , ∴ ∠CAB +∠ABD = 180°
即 ∠PAC +∠PAB +∠PBA +∠PBD = 180°.
又∠APB +∠PBA +∠PAB = 180°,
∴ ∠APB =∠PAC +∠PBD .
(2)不成立.
 (3)(a)当动点P在射线BA的右侧时,结论是
(3)(a)当动点P在射线BA的右侧时,结论是
∠PBD=∠PAC+∠APB .
(b)当动点P在射线BA上,
结论是∠PBD =∠PAC +∠APB .
或∠PAC =∠PBD +∠APB 或 ∠APB = 0°,
∠PAC =∠PBD(任写一个即可).
(c) 当动点P在射线BA的左侧时,
 结论是∠PAC =∠APB +∠PBD
.
结论是∠PAC =∠APB +∠PBD
.
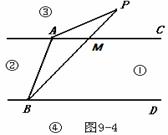
选择(a) 证明:
如图9-4,连接PA,连接PB交AC于M
∵ AC∥BD ,
∴ ∠PMC =∠PBD .
又∵∠PMC =∠PAM +∠APM ,
∴ ∠PBD =∠PAC +∠APB .
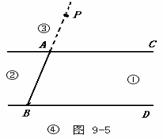
选择(b) 证明:如图9-5
 ∵ 点P在射线BA上,∴∠APB = 0°.
∵ 点P在射线BA上,∴∠APB = 0°.
∵ AC∥BD , ∴∠PBD =∠PAC .
∴ ∠PBD =∠PAC +∠APB
或∠PAC =∠PBD+∠APB
或∠APB = 0°,∠PAC =∠PBD.
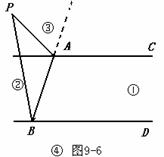
选择(c) 证明:
如图9-6,连接PA,连接PB交AC于F
∵ AC∥BD , ∴∠PFA =∠PBD .
∵ ∠PAC =∠APF +∠PFA ,
 ∴ ∠PAC =∠APB +∠PBD .
∴ ∠PAC =∠APB +∠PBD .
22. (本题满分12分)
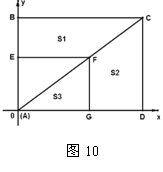
(1)S1 = S2
证明:如图10,∵ FE⊥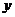 轴,FG⊥
轴,FG⊥ 轴,∠BAD = 90°,
轴,∠BAD = 90°,
∴ 四边形AEFG是矩形 .
∴ AE = GF,EF = AG .
∴ S△AEF = S△AFG ,同理S△ABC = S△ACD .
∴ S△ABC-S△AEF = S△ACD-S△AFG . 即S1 = S2 .
(2)∵FG∥CD , ∴ △AFG ∽ △ACD .
∴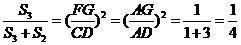 .
.
∴ FG =  CD, AG
=
CD, AG
= AD .
AD .
∵ CD = BA = 6, AD = BC = 8 , ∴ FG = 3,AG = 4 . ∴ F(4,3)。
(3)解法一:∵ △A′E′F′是由△AEF沿直线AC平移得到的 ,
∴ E′A′= E A = 3,E′F′= E F = 4 .① 如图11-1
∵ 点E′到 轴的距离与到
轴的距离与到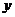 轴的距离比是5∶4 , 若点E′在第一象限 ,
轴的距离比是5∶4 , 若点E′在第一象限 ,
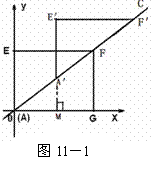 ∴设E′(4
∴设E′(4 , 5
, 5 )且
)且 > 0 ,
> 0 ,
延长E′A′交 轴于M ,得A′M = 5
轴于M ,得A′M = 5 -3, AM = 4
-3, AM = 4 .
.
∵ ∠E′=∠A′M A = 90°, ∠E′A′F′=∠ M A′A ,
∴ △ E′A′F′∽△ M A′A ,得 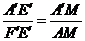 .
.
∴ 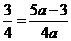 . ∴
. ∴  =
= 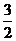 ,E′( 6,
,E′( 6, 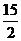 ) .
) .
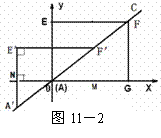
② 如图11-2
∵ 点E′到 轴的距离与到
轴的距离与到 轴的距离比是5∶4 ,
轴的距离比是5∶4 ,
若点E′在第二象限,∴设E′(-4 , 5
, 5 )且
)且 > 0,
> 0,
得NA = 4 , A′N = 3 - 5
, A′N = 3 - 5 ,
,
同理得△A′F′E′∽ △A′AN .
∴ 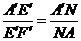 ,
, 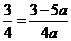 .
.
∴ a = 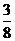 , ∴ E′(
, ∴ E′(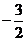 ,
, 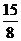 ) .
) .
 ③ 如图11-3
③ 如图11-3
∵ 点E′到 轴的距离与到
轴的距离与到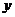 轴的距离比是5∶4 ,
轴的距离比是5∶4 ,
若点E′在第三象限,∴设E′( -4 ,- 5
,- 5 )且
)且 > 0.
> 0.
延长E′F′交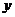 轴于点P,得AP = 5
轴于点P,得AP = 5 , P F′= 4
, P F′= 4  - 4 .
- 4 .
同理得△A′E′F′∽△A P F′ ,得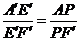 ,
,
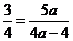 .∴
.∴  =
= 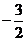 (不合舍去).
(不合舍去).
∴ 在第三象限不存在点E′.
④ 点E′不可能在第四象限 .
∴ 存在满足条件的E′坐标分别是( 6, 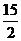 ) 、(
) 、(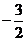 ,
, 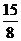 ) .
) .
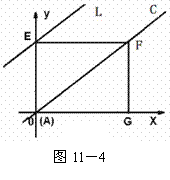 解法二:如图11-4,∵△A′E′F′是由△AEF沿直线AC平移得到的,且A′、F′两点始终在直线AC上,
解法二:如图11-4,∵△A′E′F′是由△AEF沿直线AC平移得到的,且A′、F′两点始终在直线AC上,
∴ 点E′在过点E(0,3)且与直线AC平行的直线l上移动.
∵ 直线AC的解析式是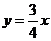 ,
,
∴ 直线l的解析式是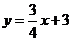 .
.
根据题意满足条件的点E′的坐标设为(4 , 5
, 5 )或( -4
)或( -4 ,5
,5 )或( -4
)或( -4 ,-5
,-5 ),其中
),其中
 > 0 .
> 0 .
∵点E′在直线l上 , ∴  或
或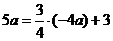 或
或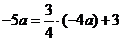
解得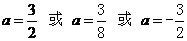 (不合舍去). ∴ E′(6,
(不合舍去). ∴ E′(6, 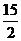 )或E′(
)或E′(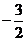 ,
, 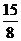 ).
).
∴ 存在满足条件的E′坐标分别是( 6 , 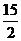 ) 、(
) 、(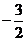 ,
, 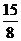 ) .
) .
解法三:
∵ △A′E′F′是由△AEF沿直线AC平移得到的,且A′、F′两点始终在直线AC上 ,
∴ 点E′在过点E(0,3)且与直线AC平行的直线l上移动 .
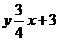 ∵ 直线AC的解析式是
∵ 直线AC的解析式是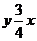 , ∴ 直线L的解析式是.
, ∴ 直线L的解析式是.
设点E′为( ,
, 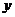 ) ∵ 点E′到
) ∵ 点E′到 轴的距离与到
轴的距离与到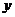 轴的距离比是5┱4 ,∴
轴的距离比是5┱4 ,∴ 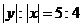 .
.
① 当 、
、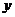 为同号时,得
为同号时,得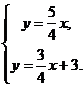 解得
解得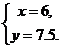 ∴ E′(6, 7.5).
∴ E′(6, 7.5).
② 当 、
、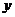 为异号时,得
为异号时,得 解得
解得 ∴ E′(
∴ E′(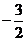 ,
, 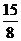 ).
).
∴存在满足条件的E′坐标分别是( 6, 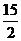 ) 、(
) 、( 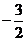 ,
, 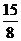 ) .
) .
 23. (本题满分14分)
23. (本题满分14分)
解:(1)∵点A横坐标为4 , ∴当  = 4时,
= 4时,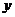 = 2 .
= 2 .
∴ 点A的坐标为( 4,2 ).
∵ 点A是直线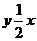 与双曲线
与双曲线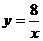 (k>0)的交点 ,
(k>0)的交点 ,
∴ k = 4 ×2 = 8 .
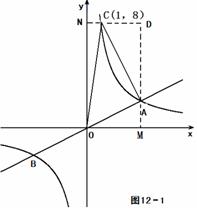
(2) 解法一:如图12-1,
∵ 点C在双曲线 上,当
上,当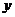 = 8时,
= 8时, = 1
= 1
∴ 点C的坐标为 ( 1, 8 ) .
过点A、C分别做 轴、
轴、 轴的垂线,垂足为M、N,得矩形DMON .
轴的垂线,垂足为M、N,得矩形DMON .
S矩形ONDM= 32 , S△ONC = 4 , S△CDA = 9, S△OAM = 4 .
S△AOC= S矩形ONDM - S△ONC - S△CDA - S△OAM =
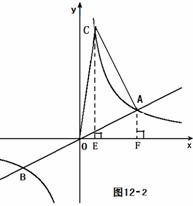 解法二:如图12-2,
解法二:如图12-2,
过点 C、A分别做 轴的垂线,垂足为E、F,
轴的垂线,垂足为E、F,
∵ 点C在双曲线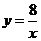 上,当
上,当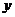 = 8时,
= 8时, = 1 .
= 1 .
∴ 点C的坐标为 ( 1, 8 ).
∵ 点C、A都在双曲线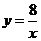 上 ,
上 ,
∴ S△COE = S△AOF = 4 。
∴ S△COE + S梯形CEFA = S△COA + S△AOF .
∴ S△COA = S梯形CEFA .
 ∵ S梯形CEFA =
∵ S梯形CEFA =  ×(2+8)×3 = 15 ,
×(2+8)×3 = 15 ,
∴ S△COA = 15 .
(3)∵ 反比例函数图象是关于原点O的中心对称图形 ,
∴ OP=OQ,OA=OB .
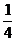 ∴ 四边形APBQ是平行四边形 .
∴ 四边形APBQ是平行四边形 .
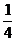 ∴ S△POA = S平行四边形APBQ = ×24 =
6 .
∴ S△POA = S平行四边形APBQ = ×24 =
6 .
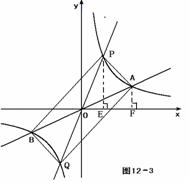
设点P的横坐标为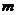 (
(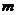 > 0且
> 0且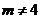 ),
),
 得P (
得P (  , ) .
, ) .
过点P、A分别做 轴的垂线,垂足为E、F,
轴的垂线,垂足为E、F,
∵ 点P、A在双曲线上,∴S△POE = S△AOF = 4 .
若0< <4,如图12-3,
<4,如图12-3,
∵ S△POE + S梯形PEFA = S△POA + S△AOF,
∴ S梯形PEFA = S△POA = 6 .
∴ 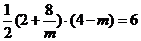 .
.
解得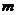 = 2,
= 2,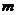 = - 8(舍去) .
= - 8(舍去) .
∴ P(2,4).
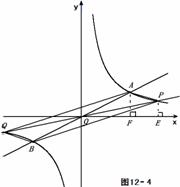
若 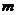 > 4,如图12-4,
> 4,如图12-4,
∵ S△AOF+ S梯形AFEP = S△AOP + S△POE,
∴ S梯形PEFA = S△POA = 6 .
∴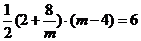 ,
,
解得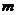 = 8,
= 8,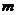 = - 2 (舍去) .
= - 2 (舍去) .
∴ P(8,1).
∴ 点P的坐标是P(2,4)或P(8,1).