摘要:②依题意,得 ≥ 1800, 即3 + 800 ≥ 1800, 解得 ≥ . 答:小俐当月至少要卖服装334件.
网址:http://m.1010jiajiao.com/timu_id_37460[举报]
先列方程,再估算出方程的解.
HB型铅笔每支0.3元,2B型铅笔每支0.5元,用4 元钱买了两种铅笔共10支,还多0.2元,问两种铅笔各买了多少支?
解:设买了HB型铅笔x支,则买2B型铅笔
这里x>0,列表如下:
从表中看出x=
查看习题详情和答案>>
HB型铅笔每支0.3元,2B型铅笔每支0.5元,用4 元钱买了两种铅笔共10支,还多0.2元,问两种铅笔各买了多少支?
解:设买了HB型铅笔x支,则买2B型铅笔
(10-x)
(10-x)
支,HB型铅笔用去了0.3x元,2B型铅笔用去了0.5(10-x)元,依题意得方程:0.3x+0.5(10-x)=4-0.2
4-0.2
.这里x>0,列表如下:
| x(支) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 0.3x+0.5(10-x)(元) | 4.8 | 4.6 | 4.4 | 4.2 | 4 | 3.8 | 3.6 | 3.4 |
6
6
是原方程的解.已知甲、乙二人从相距18千米的两地同时出发,相向而行,1
小时相遇;如果甲比乙先走
小时,那么在乙出发后1
小时两人相遇.设甲、乙二人的速度分别为x千米/小时、y千米/小时,依题意得方程组( )
| 4 |
| 5 |
| 2 |
| 3 |
| 1 |
| 2 |
阅读下列解题过程,借鉴其中一种方法解答后面给出的试题:
问题:某人买13个鸡蛋,5个鸭蛋、9个鹅蛋共用去了9.25元;买2个鸡蛋,4个鸭蛋、3个鹅蛋共用去了3.20元.试问只买鸡蛋、鸭蛋、鹅蛋各一个共需多少元.
分析:设买鸡蛋,鸭蛋、鹅蛋各一个分别需x、y、z元,则需要求x+y+z的值.由题意,知
;
视x为常数,将上述方程组看成是关于y、z的二元一次方程组,化“三元”为“二元”、化“二元”为“一元”从而获解.
解法1:视x为常数,依题意得
.
解这个关于y、z的二元一次方程组得
.
于是x+y+z=x+0.05+x+1-2x=1.05.
评注:也可以视z为常数,将上述方程组看成是关于x、y的二元一次方程组,解答方法同上,你不妨试试.
分析:视x+y+z为整体,由(1)、(2)恒等变形得5(x+y+z)+4(2x+z)=9.25,4(x+y+z)-(2x+z)=3.20.
解法2:设x+y+z=a,2x+z=b,代入(1)、(2)可以得到如下关于a、b的二元一次方
程组
.
由⑤+4×⑥,得21a+22.05,a=1.05.
评注:运用整体的思想方法指导解题.视x+y+z,2x+z为整体,令a=x+y+z,b=2x+z,代入①、②将原方程组转化为关于a、b的二元一次方程组从而获解.
请你运用以上介绍的任意一种方法解答如下数学竞赛试题:
购买五种教学用具A1、A2、A3、A4、A5的件数和用钱总数列成下表:
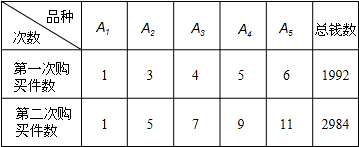
那么,购买每种教学用具各一件共需多少元? 查看习题详情和答案>>
问题:某人买13个鸡蛋,5个鸭蛋、9个鹅蛋共用去了9.25元;买2个鸡蛋,4个鸭蛋、3个鹅蛋共用去了3.20元.试问只买鸡蛋、鸭蛋、鹅蛋各一个共需多少元.
分析:设买鸡蛋,鸭蛋、鹅蛋各一个分别需x、y、z元,则需要求x+y+z的值.由题意,知
|
视x为常数,将上述方程组看成是关于y、z的二元一次方程组,化“三元”为“二元”、化“二元”为“一元”从而获解.
解法1:视x为常数,依题意得
|
解这个关于y、z的二元一次方程组得
|
于是x+y+z=x+0.05+x+1-2x=1.05.
评注:也可以视z为常数,将上述方程组看成是关于x、y的二元一次方程组,解答方法同上,你不妨试试.
分析:视x+y+z为整体,由(1)、(2)恒等变形得5(x+y+z)+4(2x+z)=9.25,4(x+y+z)-(2x+z)=3.20.
解法2:设x+y+z=a,2x+z=b,代入(1)、(2)可以得到如下关于a、b的二元一次方
程组
|
由⑤+4×⑥,得21a+22.05,a=1.05.
评注:运用整体的思想方法指导解题.视x+y+z,2x+z为整体,令a=x+y+z,b=2x+z,代入①、②将原方程组转化为关于a、b的二元一次方程组从而获解.
请你运用以上介绍的任意一种方法解答如下数学竞赛试题:
购买五种教学用具A1、A2、A3、A4、A5的件数和用钱总数列成下表:

那么,购买每种教学用具各一件共需多少元? 查看习题详情和答案>>