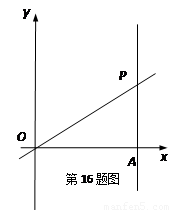摘要:∵ 点A是直线 与双曲线 的交点 ,∴ k = 4 ×2 = 8 . (2) 解法一:如图12-1.
网址:http://m.1010jiajiao.com/timu_id_37505[举报]
如图,在平面直角坐标系中,点A、B分别在x轴、y轴上,线段OA、OB的长(0A<OB)是方程组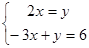 的解,点C是直线
的解,点C是直线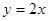 与直线AB的交点,点D在线段OC上,OD=
与直线AB的交点,点D在线段OC上,OD=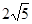
(1)求点C的坐标;
(2)求直线AD的解析式;
(3)P是直线AD上的点,在平面内是否存在点Q,使以0、A、P、Q为顶点的四边形是菱形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
如图,平面直角坐标系中,直线 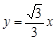 与直线
与直线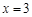 交与点P,点A是直线
交与点P,点A是直线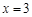 与x轴的交点,将直线OP绕着点O、直线AP绕着点A以相同的速度逆时针方向旋转,旋转过程中,两条直线交点始终为P,当直线OP与y轴正半轴重合时,两条直线同时停止转动.
与x轴的交点,将直线OP绕着点O、直线AP绕着点A以相同的速度逆时针方向旋转,旋转过程中,两条直线交点始终为P,当直线OP与y轴正半轴重合时,两条直线同时停止转动.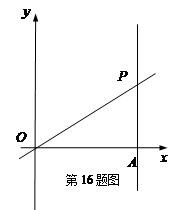
(1)当旋转角度为15°时,点P坐标为 ▲ ;
(2)整个旋转过程中,点P所经过的路线长为 ▲ .
如图,平面直角坐标系中,直线  与直线
与直线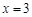 交与点P,点A是直线
交与点P,点A是直线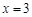 与x轴的交点,将直线OP绕着点O、直线AP绕着点A以相同的速度逆时针方向旋转,旋转过程中,两条直线交点始终为P,当直线OP与y轴正半轴重合时,两条直线同时停止转动.
与x轴的交点,将直线OP绕着点O、直线AP绕着点A以相同的速度逆时针方向旋转,旋转过程中,两条直线交点始终为P,当直线OP与y轴正半轴重合时,两条直线同时停止转动.
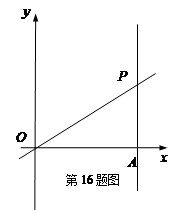
(1)当旋转角度为15°时,点P坐标为 ▲ ;
(2)整个旋转过程中,点P所经过的路线长为 ▲ . 查看习题详情和答案>>
 与直线
与直线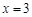 交与点P,点A是直线
交与点P,点A是直线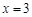 与x轴的交点,将直线OP绕着点O、直线AP绕着点A以相同的速度逆时针方向旋转,旋转过程中,两条直线交点始终为P,当直线OP与y轴正半轴重合时,两条直线同时停止转动.
与x轴的交点,将直线OP绕着点O、直线AP绕着点A以相同的速度逆时针方向旋转,旋转过程中,两条直线交点始终为P,当直线OP与y轴正半轴重合时,两条直线同时停止转动.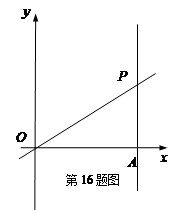
(1)当旋转角度为15°时,点P坐标为 ▲ ;
(2)整个旋转过程中,点P所经过的路线长为 ▲ . 查看习题详情和答案>>
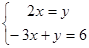 的解,点C是直线
的解,点C是直线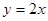 与直线AB的交点,点D在线段OC上,OD=
与直线AB的交点,点D在线段OC上,OD=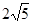
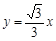 与直线
与直线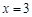 交与点P,点A是直线
交与点P,点A是直线