摘要:解法二:如图12-2.
网址:http://m.1010jiajiao.com/timu_id_37508[举报]
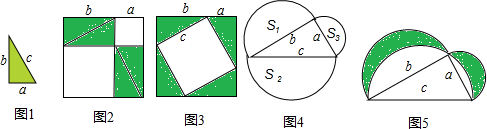
现有如图1的8张大小形状相同的直角三角形纸片,三边长分别是a、b、c.用其中4张纸片拼成如图2的大正方形(空白部分是边长分别为a和b的正方形);用另外4张纸片拼成如图3的大正方形(中间的空白部分是边长为c的正方形).
(一)观察:
从整体看,图2和图3的大正方形的面积都可以表示为(a+b)2,结论①依据整个图形的面积等于各部分面积的和.
图2中的大正方形的面积又可以用含字母a、b的代数式表示为:
图3中的大正方形的面积又可以用含字母a、b、c的代数式表示为:
(二)思考:
结合结论①和结论②,可以得到一个等式
结合结论②和结论③,可以得到一个等式
(三)应用:
请你运用(二)中得到的结论任意选择下列两个问题中的一个解答:
(1)求1.462+2×1.46×2.54+2.542的值;
(2)若分别以直角三角形三边为直径,向外作半圆(如图4),三个半圆的面积分别记作S1、S2、S3,且S1+S2+S3=20,求S2的值.
(四)延伸(本题作为附加题,做对加2分)
若分别以直角三角形三边为直径,向上作三个半圆(如图5),直角边a=5,b=12,斜边c=13,则表示图中阴影部分面积和的数值是:
请作出选择,并说明理由.
查看习题详情和答案>>

(一)观察:
从整体看,图2和图3的大正方形的面积都可以表示为(a+b)2,结论①依据整个图形的面积等于各部分面积的和.
图2中的大正方形的面积又可以用含字母a、b的代数式表示为:
a2+b2+2ab
a2+b2+2ab
,结论②图3中的大正方形的面积又可以用含字母a、b、c的代数式表示为:
c2+2ab
c2+2ab
,结论③(二)思考:
结合结论①和结论②,可以得到一个等式
(a+b)2=a2+b2+2ab
(a+b)2=a2+b2+2ab
;结合结论②和结论③,可以得到一个等式
a2+b2=c2
a2+b2=c2
;(三)应用:
请你运用(二)中得到的结论任意选择下列两个问题中的一个解答:
(1)求1.462+2×1.46×2.54+2.542的值;
(2)若分别以直角三角形三边为直径,向外作半圆(如图4),三个半圆的面积分别记作S1、S2、S3,且S1+S2+S3=20,求S2的值.
(四)延伸(本题作为附加题,做对加2分)
若分别以直角三角形三边为直径,向上作三个半圆(如图5),直角边a=5,b=12,斜边c=13,则表示图中阴影部分面积和的数值是:
A
A
A.有理数 B.无理数 C.无法判断请作出选择,并说明理由.
(2012•盐田区二模)东海中学九年级共12个班,各48名学生,对其学业水平测试成绩进行抽样分析.
(1)收集数据:从全年级学生中抽取一个48人的样本:(A)随机抽取一个班的48名学生;(B)在全年级随机抽取48名学生;(C)在全年级12个班中各随机抽取4名学生.其中合理的抽样方法的序号是
(2)整理数据:将抽取的48名学生的成绩进行分组,并制作出如下不完整的频数分布表和扇形统计图.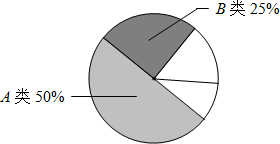
①直接写出A类部分的频数;②直接写出B类部分的频率;③直接写出C类部分的圆心角的度数;④估计D类学生的人数.
(3)分析数据:将东海、南山两所中学的抽样数据进行对比,得下表:
你认为哪所学校的成绩较好?结合数据提出一个解释来支持你的观点.
查看习题详情和答案>>
(1)收集数据:从全年级学生中抽取一个48人的样本:(A)随机抽取一个班的48名学生;(B)在全年级随机抽取48名学生;(C)在全年级12个班中各随机抽取4名学生.其中合理的抽样方法的序号是
B、C
B、C
(注:把你认为合理的抽样方法的序号都写上).(2)整理数据:将抽取的48名学生的成绩进行分组,并制作出如下不完整的频数分布表和扇形统计图.

| 成绩(单位:分) | 频数 | 频率 |
| A类(80~100) | 1/2 | |
| B类(60~79) | 12 | |
| C类(40~59) | 8 | 1/6 |
| D类(0~39) | 4 | 1/12 |
(3)分析数据:将东海、南山两所中学的抽样数据进行对比,得下表:
| 学校 | 平均数(分) | 极差(分) | 方差 | A、B类的频率和 |
| 东海中学 | 71 | 52 | 432 | 0.75 |
| 南山中学 | 71 | 80 | 497 | 0.82 |
欧洲中世纪,赌博之风盛行,赌徒们最感兴趣的是赌博的输赢,比如在掷骰子的赌博中,他们最关心哪种结果发生的可能性更大一些.对这些求机会游戏中可能性大小的问题,当时人们仅仅停留在经验认识的阶段,还不能作出理论上的答复,这就刺激当时的一些数学家去思考、研究它们,从而促使一门新的数学分支——概率论的产生.可以说,概率起源于赌博.
那个时候提出的一些概率问题,多数与赌博有关.下面我们用学过的“树状图”来解决下面这个有名的赌博问题.
17世纪的一天,法国的赌徒保罗与好赌的贵族梅雷相约赌钱.他们两人各拿出6枚金币,然后掷骰子,约定赌5局,谁先胜3局就可得到12枚金币.比赛开始后,保罗连胜了两局,接着梅雷胜一局.这时,梅雷得到通知,要他马上去陪同国王接见贵宾,赌博只好中止.以后二人又不愿意继续赌下去.问:这12枚金币二人应怎样分配才合理?
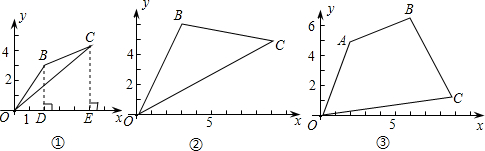
(2007•海淀区二模)例.如图①,平面直角坐标系xOy中有点B(2,3)和C(5,4),求△OBC的面积.
解:过点B作BD⊥x轴于D,过点C作CE⊥x轴于E.依题意,可得
S△OBC=S梯形BDEC+S△OBD-S△OCE
=
(BD+CE)(OE-OD)+
OD•BD-
•OE•CE
=
×(3+4)×(5-2)+
×2×3-
×5×4=3.5.
∴△OBC的面积为3.5.
(1)如图②,若B(x1,y1)、C(x2,y2)均为第一象限的点,O、B、C三点不在同一条直线上.仿照例题的解法,求△OBC的面积(用含x1、x2、y1、y2的代数式表示);
(2)如图③,若三个点的坐标分别为A(2,5),B(7,7),C(9,1),求四边形OABC的面积.
查看习题详情和答案>>
解:过点B作BD⊥x轴于D,过点C作CE⊥x轴于E.依题意,可得
S△OBC=S梯形BDEC+S△OBD-S△OCE
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴△OBC的面积为3.5.
(1)如图②,若B(x1,y1)、C(x2,y2)均为第一象限的点,O、B、C三点不在同一条直线上.仿照例题的解法,求△OBC的面积(用含x1、x2、y1、y2的代数式表示);
(2)如图③,若三个点的坐标分别为A(2,5),B(7,7),C(9,1),求四边形OABC的面积.

(本题满分10分) 下表是2011年12月的日历表,请解答问题:在表中用形如下图的平行四边形框框出4个数,
⑴若框出的4个数的和为74,请你通过列方程的办法,求出它分别是哪4天?
⑵框出的4个数的和可能是26吗?为什么?
| 星期日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 |
|
|
|
|
| 1 | 2 | 3 |
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
查看习题详情和答案>>
