6、函数与方程在导数中的应用
例9.(2008湖南卷,理21)已知函数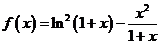 .
.
(I) 求函数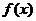 的单调区间;
的单调区间;
(Ⅱ)若不等式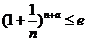 对任意的
对任意的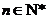 都成立(其中e是自然对数的底数).
都成立(其中e是自然对数的底数).
求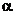 的最大值.
的最大值.
分析:由导数研究函数的单调性,求得函数的单调区间,不等式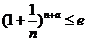 对任意的
对任意的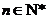 都成立可等价转化为不等式
都成立可等价转化为不等式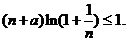 进而分离出
进而分离出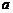 来,不等式恒成立转为函数研究最值问题,可构造函数利用导数研究函数的单调性,从而求出最值。
来,不等式恒成立转为函数研究最值问题,可构造函数利用导数研究函数的单调性,从而求出最值。
解: (Ⅰ)函数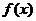 的定义域是
的定义域是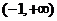 ,
,
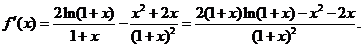
设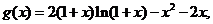 则
则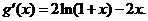
令 则
则
当 时,
时, 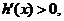
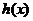 在(-1,0)上为增函数,
在(-1,0)上为增函数,
当x>0时,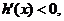
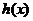 在
在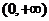 上为减函数.
上为减函数.
所以h(x)在x=0处取得极大值,而h(0)=0,所以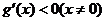 ,
,
函数g(x)在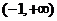 上为减函数.
上为减函数.
于是当 时,
时,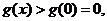
当x>0时,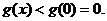
所以,当 时,
时,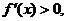
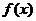 在(-1,0)上为增函数.
在(-1,0)上为增函数.
当x>0时,
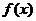 在
在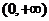 上为减函数.
上为减函数.
故函数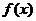 的单调递增区间为(-1,0),单调递减区间为
的单调递增区间为(-1,0),单调递减区间为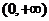 .
.
(Ⅱ)不等式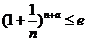 等价于不等式
等价于不等式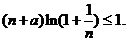 由
由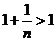 知,
知,
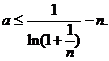 设
设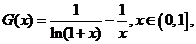 则
则
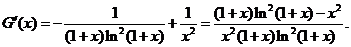
由(Ⅰ)知,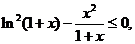 即
即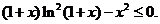
所以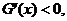
 于是G(x)在
于是G(x)在 上为减函数.
上为减函数.
故函数G(x)在 上的最小值为
上的最小值为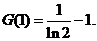
所以a的最大值为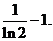
评注:第(1)问是为第二问铺垫的,在解答问题(2)时,不等式恒成立问题转化为函数研究最值,利用导数研究单调性,进而研究最值是解决函数最值问题的常用方法。理科的题目常常是超越方程或不等式,要利用导数解答问题。而文科的题基本上是含有参数的三次函数,如下一例题
例10.(2008北京卷,文17)已知函数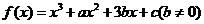 ,且
,且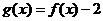 是奇函数.(Ⅰ)求
是奇函数.(Ⅰ)求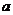 ,
, 的值;(Ⅱ)求函数
的值;(Ⅱ)求函数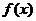 的单调区间.
的单调区间.
分析:本题从函数的性质入手,利用奇函数的定义,确定函数的解析式,,再由导数研究函数的单调性。
解:(Ⅰ)因为函数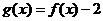 为奇函数,
为奇函数,
所以,对任意的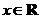 ,
,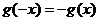 ,即
,即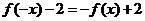 .
.
又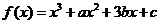
所以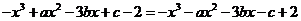 .
.
所以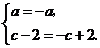
解得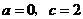 .
.
(Ⅱ)由(Ⅰ)得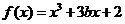 .
.
所以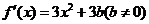 .
.
当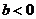 时,由
时,由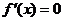 得
得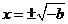 .
.
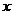 变化时,
变化时, 的变化情况如下表:
的变化情况如下表:
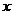 |
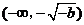 |
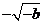 |
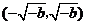 |
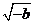 |
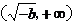 |
 |
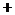 |
0 |
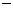 |
0 |
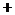 |
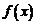 |
单调递增 |
极大值 |
单调递减 |
极小值 |
单调递增 |
所以,当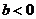 时,函数
时,函数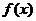 在
在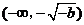 上单调递增,在
上单调递增,在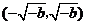 上单调递减,在
上单调递减,在 上单调递增.
上单调递增.
当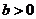 时,
时,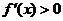 ,所以函数
,所以函数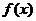 在
在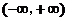 上单调递增.
上单调递增.
评注: 为奇函数是对任意的
为奇函数是对任意的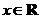 ,
,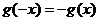 都成立来说的,也就是恒等式,对应项的系数相等,从而确定系数。在研究含有参数的函数的单调性时往往要对参数在分界值处进行分类讨论。
都成立来说的,也就是恒等式,对应项的系数相等,从而确定系数。在研究含有参数的函数的单调性时往往要对参数在分界值处进行分类讨论。
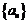 中,
中,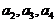 分别是某等差数列的第5项,第3项,第2项,且
分别是某等差数列的第5项,第3项,第2项,且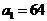 ,公比
,公比 ;
;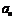 (2)设
(2)设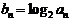 ,求数列
,求数列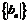 的前n项和
的前n项和 。
。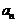 ,从而得到
,从而得到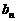 ,在求数列
,在求数列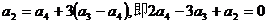
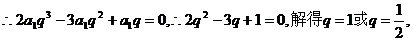
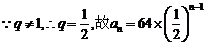

 ,
,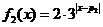 (
(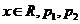 为常数).函数
为常数).函数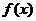 定义为:对每个给定的实数
定义为:对每个给定的实数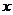 ,
,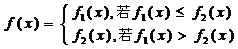
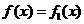 对所有实数
对所有实数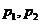 表示);
表示);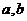 是两个实数,满足
是两个实数,满足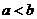 ,且
,且 .若
.若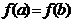 ,求证:函数
,求证:函数 上的单调增区间的长度之和为
上的单调增区间的长度之和为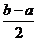 (闭区间
(闭区间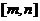 的长度定义为
的长度定义为 )
)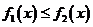 (对所有实数
(对所有实数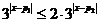 ,即
,即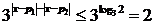 对所有实数
对所有实数 的最大值为
的最大值为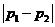 ,
,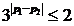 ,即
,即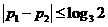 ,这就是所求的充分必要条件。
,这就是所求的充分必要条件。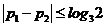 时,由(1)知
时,由(1)知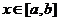 )
) 则由
则由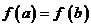 及
及 易知
易知 ,
, 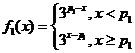 的单调性可知,
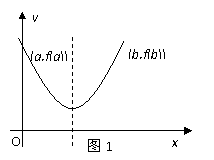
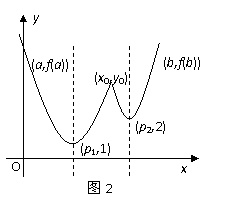
的单调性可知,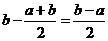 (参见示意图1)
(参见示意图1)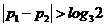 时,不妨设
时,不妨设 ,则
,则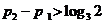 ,于是
,于是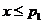 时,有
时,有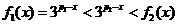 ,从而
,从而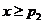 时,有
时,有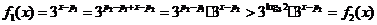
 从而
从而
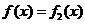 ;当
;当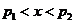 时,
时,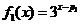 ,及
,及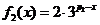 ,由方程
,由方程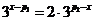 解得
解得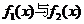 图象交点的横坐标为
图象交点的横坐标为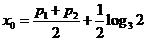 ⑴
⑴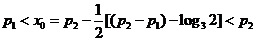 ,
,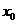 在
在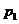 与
与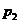 之间。由⑴易知
之间。由⑴易知 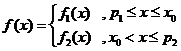
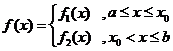 (参见示意图2)
(参见示意图2)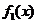 及
及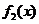 的单调性可知,
的单调性可知,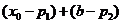 ,由于
,由于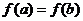 ,即
,即 ,得
,得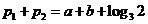 ⑵
⑵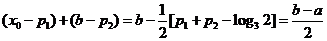
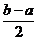 。
。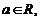 且
且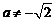 ,比较
,比较 与
与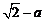 的大小.
的大小.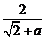 -(
-(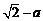 )=
)=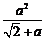 ,
,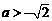 且
且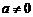 时,∵
时,∵ 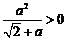 ,∴
,∴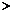
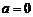 时, ∵
时, ∵ 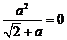 ,∴
,∴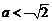 时,∵
时,∵ 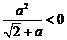 ,∴
,∴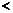
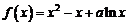
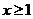 时,
时,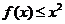 恒成立,求
恒成立,求 的取值范围;
的取值范围;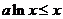 在
在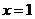 时
时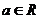 ,当
,当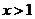 时即
时即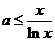 ,令
,令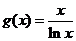 ,
,
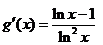
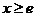 时
时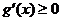 ,
,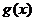 在
在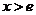 时为增函数,
时为增函数,
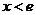 时为减函数
时为减函数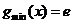 ∴
∴ 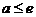
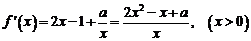
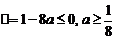 时,
时,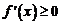 恒成立,
恒成立,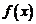 在
在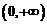 上为增函数.
上为增函数.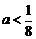 时,①当
时,①当 时,
时,
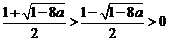 ,
,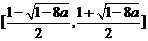 上为减函数,
上为减函数,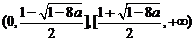 上为增函数。②当
上为增函数。②当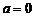 时,
时,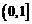 上为减函数,
上为减函数,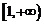 上为增函数.
上为增函数. 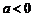 时,
时,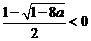 ,故
,故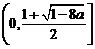 ]上为减函数,
]上为减函数,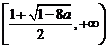 上为增函数.
上为增函数.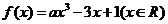 ,若对于任意的
,若对于任意的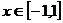 都有
都有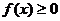 成立,则实数
成立,则实数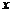 的正负进行讨论,转为
的正负进行讨论,转为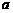 的不等式,然后可以通过求导研究右边关于
的不等式,然后可以通过求导研究右边关于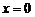 ,则不论
,则不论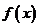 ≥0显然成立;当
≥0显然成立;当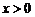 即
即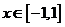 时,
时, ≥0可化为:
≥0可化为: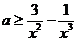
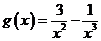 ,则
,则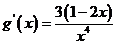 ,
所以
,
所以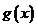 在区间
在区间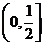 上单调递增,在区间
上单调递增,在区间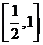 上单调递减,因此
上单调递减,因此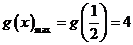 ,从而
,从而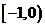 时,
时,
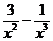 ,
,
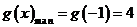 ,从而
,从而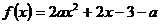 ,如果函数
,如果函数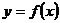 在区间
在区间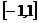 上有零点,求
上有零点,求 ,
, 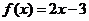 ,显然在
,显然在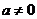 .
. , 解得
, 解得 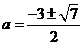
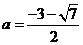 时,
时, 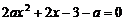 的解为
的解为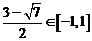 ,
,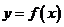 恰有一个零点在
恰有一个零点在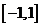 上;
上; ,即
,即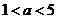 时,
时,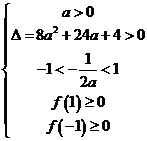 或
或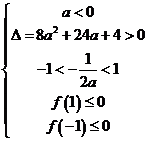
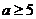 或
或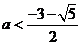 ,综上所求实数
,综上所求实数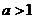 或
或 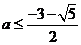 .
.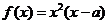 。
。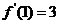 ,求
,求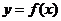 在点
在点 处的切线方程;
处的切线方程;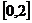 上的最大值。
上的最大值。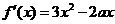 ,因为
,因为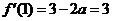 ,所以
,所以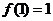 ,
,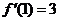 ,所以曲线
,所以曲线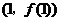 处的切线方程为
处的切线方程为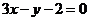 .
.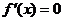 ,解得
,解得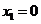 ,
,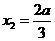 .
.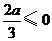 ,即
,即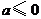 时,
时,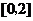 上单调递增,从而
上单调递增,从而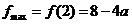 .
.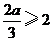 ,即
,即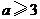 时,
时,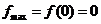 .
.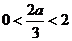 ,即
,即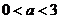 时,
时,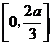 上单调递减,在
上单调递减,在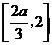 上单调递增,从而
上单调递增,从而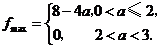 综上所述,
综上所述, 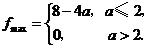
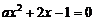 至少有一个正的实根的充要条件是 ( )
至少有一个正的实根的充要条件是 ( )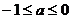 B.
B.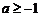 C.
C.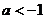 D.
D.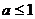
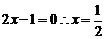 ,满足。当
,满足。当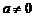 时,
时,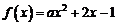 ,当
,当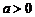 时,∵
时,∵ ,∴
,∴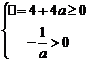 即
即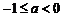 ,综上
,综上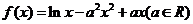 .
.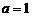 时,证明函数
时,证明函数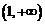 上是减函数,求实数
上是减函数,求实数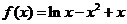 ,其定义域是
,其定义域是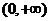 ,
,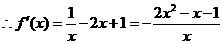 令
令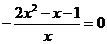 ,
, 或
或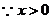 ,
,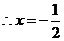 舍去.
舍去.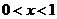 时,
时,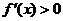 ;当
;当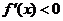 .
.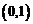 上单调递增,在区间
上单调递增,在区间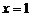 时,函数
时,函数 .
.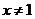 时,
时,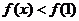 ,即
,即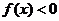 . ∴函数
. ∴函数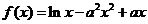 其定义域为
其定义域为 所以
所以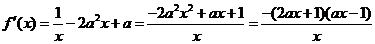
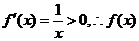 在区间
在区间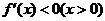 等价于
等价于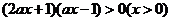 ,即
,即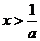 .
.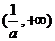 .依题意,得
.依题意,得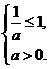 解之得
解之得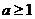 .
. 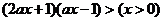 ,即
,即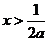 ·
· ,
,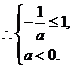 得
得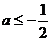
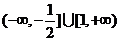
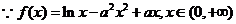
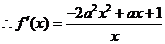
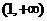 上是减函数,可得
上是减函数,可得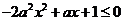 在区间
在区间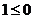 不合题意
不合题意 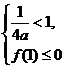 即
即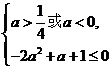
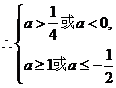
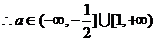
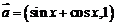 ,
,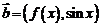 ,其中
,其中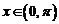 ,
,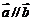 ,则函数
,则函数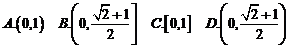
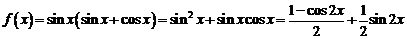
 ,∵
,∵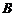
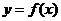 是顶点在原点的二次函数,且方程
是顶点在原点的二次函数,且方程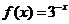 有一个根
有一个根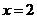 ,则不等式
,则不等式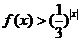 的解集是(
)
的解集是(
)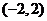 B.
B.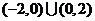 C.
C.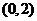 D.
D.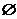
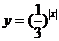 的图象和对称性解答问题。
的图象和对称性解答问题。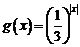 为偶函数,其图象也关于原点对称,又方程
为偶函数,其图象也关于原点对称,又方程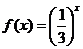 有一个根
有一个根 时,不等式
时,不等式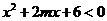 恒成立,则
恒成立,则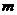 的取值范围是
的取值范围是
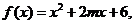
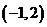 上函数
上函数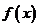 的图象位于
的图象位于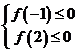 即
即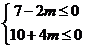 ,解得
,解得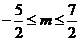 .
.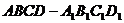 棱长为1,
棱长为1,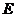 为棱
为棱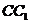 上的动点.
上的动点.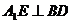 ;
;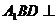 平面
平面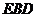 ;
;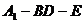 的大小为
的大小为 ?若存在,确定其位置,若不存在,说明理由.
?若存在,确定其位置,若不存在,说明理由. 分析:利用有关垂直的判定定理判定,在此基础上解决(3),可以设为
分析:利用有关垂直的判定定理判定,在此基础上解决(3),可以设为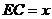 ,求的
,求的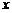 的方程解出。
的方程解出。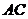 ,则
,则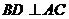 ,
,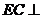 平面
平面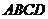 ,
,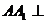 平面
平面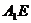 在平面
在平面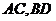 交于点O,连结
交于点O,连结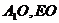 ,
,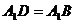 ,∴
,∴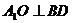 ,同理可证
,同理可证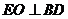 ,
,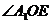 是二面角
是二面角 ,
,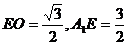 ,∴
,∴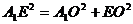 ,
,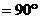 ,∴平面
,∴平面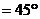 .设
.设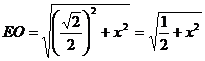 ,
,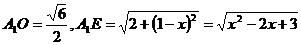 ,
, 中,由余弦定理得:
中,由余弦定理得: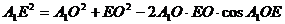 ,
,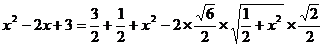 ,可化为
,可化为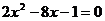 ,
,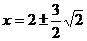 ,由于
,由于
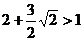 ,
, :
: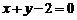 上任取一点M,使过M且以双曲线
上任取一点M,使过M且以双曲线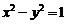 的焦点为焦点的椭圆C的长轴最短
的焦点为焦点的椭圆C的长轴最短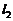 :
: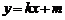 与椭圆C相交于A、B两点(A、B不是椭圆的顶点),以
与椭圆C相交于A、B两点(A、B不是椭圆的顶点),以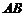 为直径的圆过椭圆的上顶点,求证:直线
为直径的圆过椭圆的上顶点,求证:直线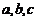 的值,从而求得椭圆方程,并通过解方程组研究直线与椭圆的位置关系, 以
的值,从而求得椭圆方程,并通过解方程组研究直线与椭圆的位置关系, 以 ,∴椭圆C的焦点为
,∴椭圆C的焦点为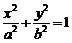 ,
,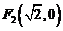 关于直线
关于直线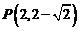 ,连接
,连接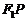 交直线
交直线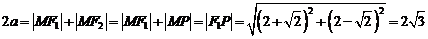 ,∴
,∴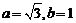 ∴椭圆的方程为
∴椭圆的方程为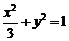 ,椭圆的上顶点为
,椭圆的上顶点为
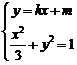 得
得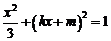 ,即
,即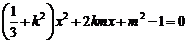 ,
,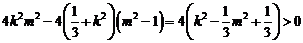 ,即
,即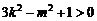 ,
,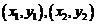 ,则
,则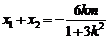 ,
,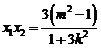 ,
,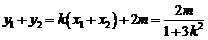 ,
,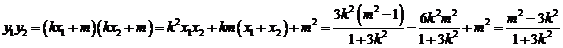 ∵以
∵以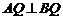 ∴
∴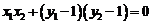 ,
,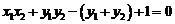 ,∴
,∴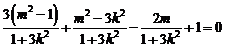 ,化简得
,化简得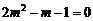 ,∴
,∴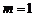 或
或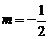 .当
.当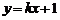 过定点
过定点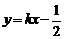 过定点
过定点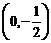 ,∴直线
,∴直线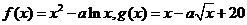 ,且
,且 处取极值.
处取极值.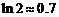 )
)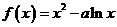 ,∴
,∴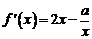 ,∵
,∵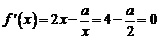 ∴
∴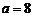 …………………………………………… 2分
…………………………………………… 2分 ∴
∴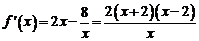
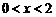 时,
时,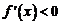 ,
, 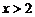 时,
时, 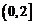 , 增区间为
, 增区间为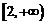 .………4分
.………4分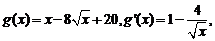
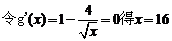 .
.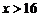 时,
时, 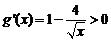 ∴
∴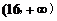 上为增函数;
上为增函数;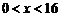 时,
时, , ∴
, ∴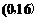 上为减函数.
上为减函数.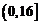 , 增区间为
, 增区间为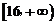
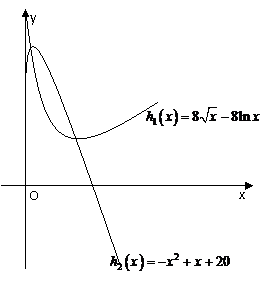 (Ⅱ)
(Ⅱ)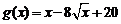 的图象的交点个数,
的图象的交点个数,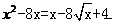
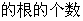
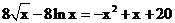 ,设
,设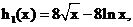
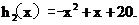
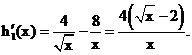
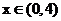 时,
时, 为减函数.
为减函数.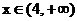 时,
时,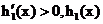 为增函数.
为增函数.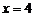 时
时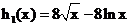 最小,
最小,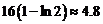 而
而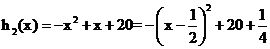 的
的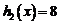
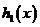 与
与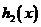 的大致图象如图:
的大致图象如图: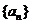 的首项
的首项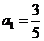 ,
,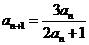 ,
,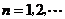 .
.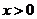 ,
,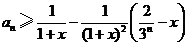 ,
,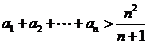 .
.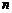 ,右边含有
,右边含有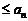 。
。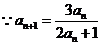 ,
,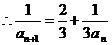 ,
,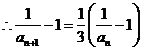 ,
,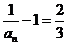 ,
, 是以
是以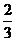 为首项,
为首项,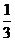 为公比的等比数列.
为公比的等比数列.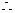
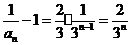 ,
, .
.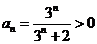 ,
,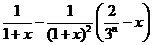
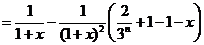
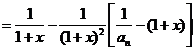
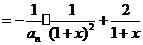
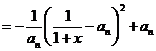
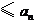 ,
,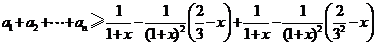
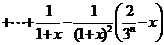
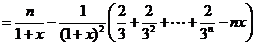 .
.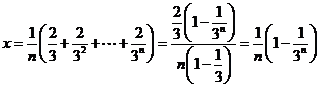 ,
,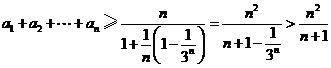 .
.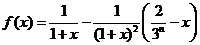 ,
,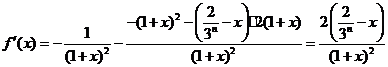
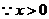 ,
,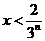 时,
时,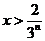 时,
时, ,
,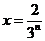 时,
时,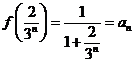 .
.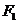 、
、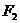 分别是椭圆
分别是椭圆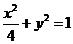 的左、右焦点.
的左、右焦点.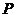 是该椭圆上的一个动点,求
是该椭圆上的一个动点,求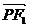
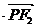 的最大值和最小值;
的最大值和最小值; 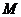
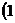 ,
,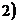 的直线
的直线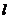 与椭圆交于两不同的点
与椭圆交于两不同的点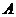 、
、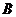 ,且
,且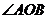 为锐角(其中
为锐角(其中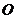 为坐标原点),求直线
为坐标原点),求直线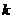 的取值范围.
的取值范围.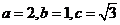
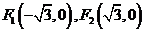 ,设
,设
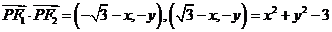
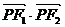
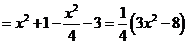
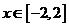 ,故当
,故当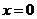 ,即点
,即点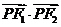 有最小值
有最小值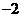
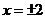 ,即点
,即点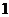 .
. 
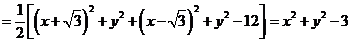
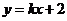 ,设
,设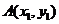 ,
,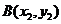
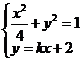 得
得
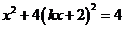
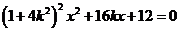
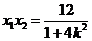 ,
,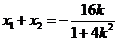
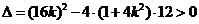
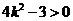 解得
解得
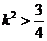 ①
① 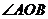 为锐角
为锐角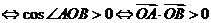


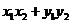
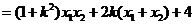
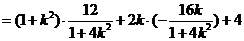
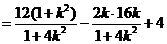

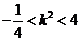 ②
②
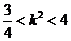
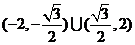 .
. 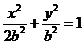 ,抛物线方程为
,抛物线方程为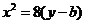 .如图4所示,过点
.如图4所示,过点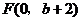 作
作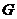 ,已知抛物线在点
,已知抛物线在点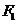 .
. 分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点
分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点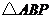 为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).
为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).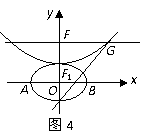 :(1)由
:(1)由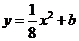 ,当
,当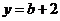 得
得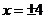 ,
,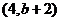 ,
,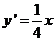 ,
,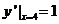 ,
,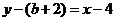 即
即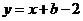 ,
,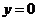 得
得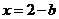 ,
,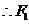 点的坐标为
点的坐标为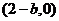 ,由椭圆方程得
,由椭圆方程得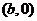 ,
,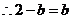 即
即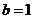 ,即椭圆和抛物线的方程分别为
,即椭圆和抛物线的方程分别为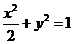 和
和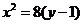 ;
; 过
过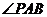 为直角的
为直角的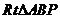 只有一个,同理
只有一个,同理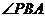 为直角的
为直角的 为直角,设
为直角,设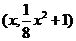 ,
,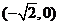 和
和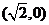 ,
,
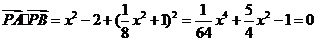 。关于
。关于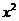 的二次方程有一大于零的解,
的二次方程有一大于零的解,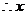 有两解,即以
有两解,即以 为直角三角形。
为直角三角形。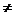 x2),则y21=4x1, y22=4x2,
x2),则y21=4x1, y22=4x2,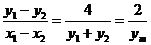 .从而AB的垂直平分线l的方程为
.从而AB的垂直平分线l的方程为 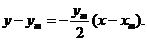
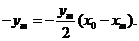
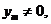 于是
于是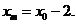 故点P(x0,0)的所有“相关弦”的中点的横坐标都是x0-2.
故点P(x0,0)的所有“相关弦”的中点的横坐标都是x0-2.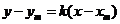 ,代入
,代入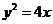 中,
中,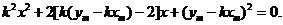 (·)
(·)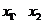 是方程(·)的两个实根,且
是方程(·)的两个实根,且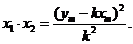
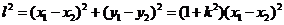
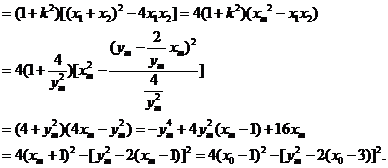
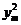 <4xm=4(xm-2)
=4x0-8,于是设t=
<4xm=4(xm-2)
=4x0-8,于是设t=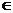 (0,4x0-8).
(0,4x0-8).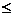 0,g(t)在区间(0,4 x0-8)上是减函数,
0,g(t)在区间(0,4 x0-8)上是减函数,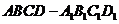 的对角线
的对角线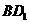 上.过点
上.过点 的直线,与正方体表面相交于
的直线,与正方体表面相交于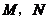 .设
.设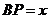 ,
,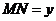 ,
,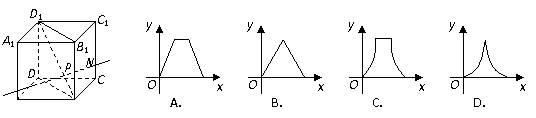 则函数
则函数
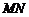 的特殊性与平面
的特殊性与平面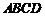 内作正投影,保持其长度不变,从而把空间问题转为平面问题,在平面内研究函数关系即可顺利完成。
内作正投影,保持其长度不变,从而把空间问题转为平面问题,在平面内研究函数关系即可顺利完成。 解:设正方体的棱长为
解:设正方体的棱长为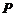 点始终是
点始终是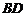 的中点滑动,
的中点滑动,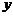 值逐渐增大到最大,再由中
值逐渐增大到最大,再由中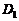 点滑动,而逐渐变小,排除
点滑动,而逐渐变小,排除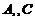 ,把
,把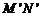 ,则
,则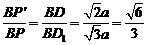 ,
,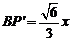 ,所以当
,所以当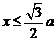 时,
时,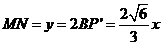 为一次函数,故选
为一次函数,故选