摘要:变量对不等式变形的影响 例5..设函数.若对于任意的都有成立.则实数的值为 分析:若对于任意的都有成立.不等式恒成立求参数的范围.可将参数分化出来.在分离时需要对其系数的正负进行讨论.转为的不等式.然后可以通过求导研究右边关于的函数.判断其单调性并求出其最值. 解:若.则不论取何值.≥0显然成立,当 即时.≥0可化为: 设.则. 所以 在区间上单调递增.在区间上单调递减.因此.从而≥4, 当x<0 即时.≥0可化为. 在区间上单调递增.因此.从而≤4.综上=4 答案:4 评注:本小题考查不等式的转化和函数单调性的综合运用.对于不等式恒成立问题常常要将参数分离出来.转化为研究函数的最值.通过求导研究函数的单调性和最值.在情况不定时对其取值进行分类讨论.
网址:http://m.1010jiajiao.com/timu_id_3980608[举报]
三个同学对问题“关于x的不等式x2+25+|x3-5x2|≥ax在[1,12]上恒成立,求实数a的取值范围”提出各自的解题思路.
甲说:“只须不等式左边的最小值不小于右边的最大值”.
乙说:“把不等式变形为左边含变量x的函数,右边仅含常数,求函数的最值”.
丙说:“把不等式两边看成关于x的函数,作出函数图象”.
参考上述解题思路,你认为他们所讨论的问题的正确结论,即a的取值范围是 .
查看习题详情和答案>>
甲说:“只须不等式左边的最小值不小于右边的最大值”.
乙说:“把不等式变形为左边含变量x的函数,右边仅含常数,求函数的最值”.
丙说:“把不等式两边看成关于x的函数,作出函数图象”.
参考上述解题思路,你认为他们所讨论的问题的正确结论,即a的取值范围是
(06年上海卷理)三个同学对问题“关于![]() 的不等式
的不等式![]() +25+|
+25+|![]() -5
-5![]() |≥
|≥![]() 在[1,12]上恒成立,求实数
在[1,12]上恒成立,求实数![]() 的取值范围”提出各自的解题思路.
的取值范围”提出各自的解题思路.
甲说:“只须不等式左边的最小值不小于右边的最大值”.
乙说:“把不等式变形为左边含变量![]() 的函数,右边仅含常数,求函数的最值”.
的函数,右边仅含常数,求函数的最值”.
丙说:“把不等式两边看成关于![]() 的函数,作出函数图像”.
的函数,作出函数图像”.
参考上述解题思路,你认为他们所讨论的问题的正确结论,即![]() 的取值范围是 .
的取值范围是 .
查看习题详情和答案>>
三个同学对问题“关于x的不等式x2+25+|x3-5x2|≥ax在[1,12]上恒成立,求实数a的取值范围”提出各自的解题思路.
甲说:“只需不等式左边的最小值不小于右边的最大值.”
乙说:“把不等式变形为左边含变量x的函数,右边仅含常数,求函数的最值.”
丙说:“把不等式两边看成关于x的函数,作出函数图象.”
参考上述解题思路,你认为他们所讨论的问题的正确结论,即a的取值范围是__________.
查看习题详情和答案>>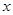 的不等式
的不等式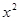 +25+|
+25+|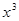 -5
-5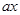 在[1,12]上恒成立,求实数
在[1,12]上恒成立,求实数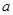 的取值范围”提出各自的解题思路.
的取值范围”提出各自的解题思路.